YEAHx4YEAHx4
PS

PCA

주성분 분석, Principal Component Analysis

YEAHx4

YEAHx4

2025-08-20
15 mins

차원의 저주

많은 데이터는 고차원 공간에 존재합니다. 즉, 굉장히 많은 feature로 이루어져 있습니다. 하지만, 고차원에서는 우리의 직관과는 다른 현상이 발생합니다. 예를 들어, 2D의 단위면적에서 임의로 두 점을 찍었을 때, 두 점 사이의 거리의 기댓값은 다음처럼 구할 수 있습니다.

\[ \mathbb{E}[d] = \int_0^1 \int_0^1 \int_0^1 \int_0^1 \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2} \, dx_1 \, dx_2 \, dy_1 \, dy_2 \]

이 식은 수학적 기교로 계산할 수 있긴 하지만 고차원으로 확장하기 어려우니 파이썬을 통해 통계적으로 근삿값을 구하겠습니다. 몬테-카를로 방법이라고도 합니다.

import numpy as np

def dist(n, trials=1_000_000, seed=None):
    rng = np.random.default_rng(seed)
    A = rng.random((trials, n))
    B = rng.random((trials, n))
    return np.linalg.norm(A - B, axis=1).mean()

print(dist(2, seed=42)) # 0.521109890202126

대략 0.52 정도의 값이 나옵니다. 차원이 커진다면 어떨까요?

import matplotlib.pyplot as plt

dims = range(2, 101)
values = [dist(n, seed=42, trials=10_000) for n in dims]

plt.figure(figsize=(8,5))
plt.plot(dims, values)
plt.xlabel("Dimension (n)")
plt.ylabel("Expected Distance")
plt.title("Monte Carlo Estimate of $E[d]$ in $[0,1]^n$")
plt.grid(True)
plt.show()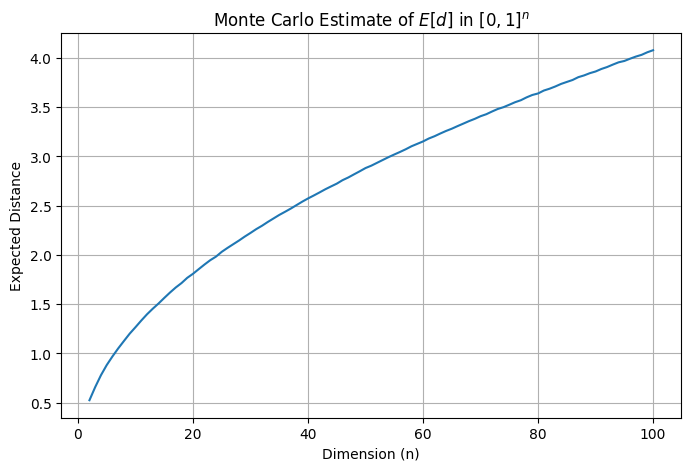

Expected distance

점점 점들 사이의 평균 거리가 멀어지는 것을 볼 수 있습니다. 1,000,000 차원에서는 평균 거리가 408 정도로 매우 커집니다. 즉, 차원이 클 수록 데이터가 멀리 퍼져 희소(sparse)해집니다. 이렇게 굉장히 많은 feature는 모델의 학습을 느리게 할 뿐 아니라 좋은 솔루션을 찾기 힘들게 만듭니다. 이를 차원의 저주(curse of dimensionality)라고 합니다. 이 문제를 해결하는 한 방법은 데이터를 추가하는 것입니다. 하지만, 차원이 많을 때는 필요한 데이터도 기하급수적으로 늘어납니다. 다른 방법으로는 차원 자체를 줄일 수 있습니다. 많은 경우 모든 차원이 필요하지 않습니다. 몇 차원을 제거하더라도 데이터에 큰 손실이 없는 경우가 많습니다. 이것을 차원 축소(dimensionality reduction)라고 하고 차원 축소의 대표적인 기법이 PCA입니다.

PCA

차원 축소는 여러 방법으로 할 수 있습니다. PCA는 투영(projection)을 사용해서 차원을 축소합니다. 아래 함수로 만들어진 데이터가 있다고 해 봅시다.

angle = np.pi / 5
stretch = 5
m = 200

np.random.seed(3)
X = np.random.randn(m, 2) / 10
X = X @ np.array([[stretch, 0], [0, 1]])
X = X @ [[np.cos(angle), np.sin(angle)],
        [np.sin(angle), np.cos(angle)]]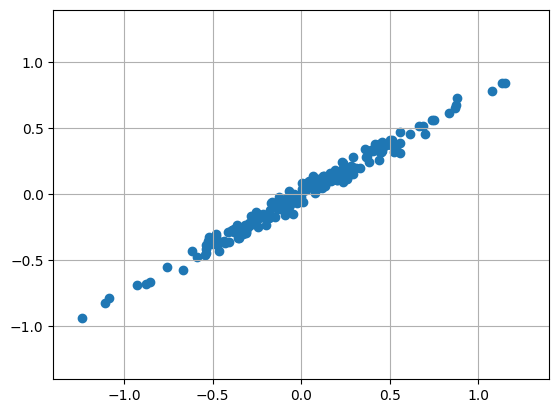

Scatter plot

\( m = 200 \)개의 데이터를 만들어 \( x_1 \) 방향으로 늘린 후 회전 행렬을 통해 \( \pi / 5 \)만큼 돌려 주었습니다. 각 데이터는 \( x_1, x_2 \)로 표현되는 2차원 데이터입니다. 그런데 2차원 보단 1차원 데이터처럼 생겼습니다. 저희의 목표는 이 2차원 데이터를 1차원으로 축소하는 것입니다. 아까 PCA는 투영을 사용한다고 했습니다. 그런데, 어디다 투영해야 할까요? 아래 그래프는 다양한 축을 기준으로 투영한 결과입니다.

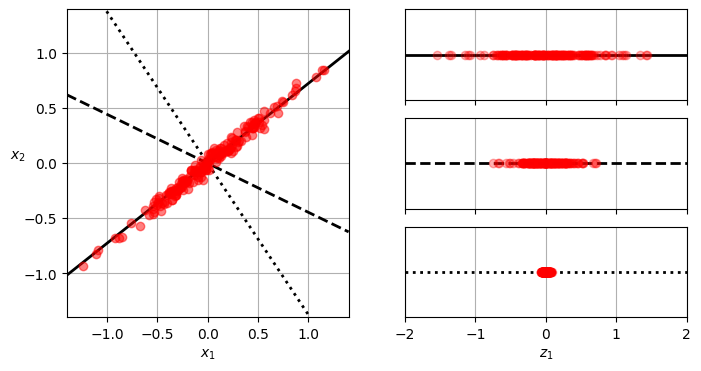
Projection graph

위 그래프를 보면 어떤 축 \( z_1 \)을 잡고 그 위에 데이터들을 투영했습니다. 어느 방향으로 투영하느냐에 따라 데이터가 멀리 퍼져있기도 하고 거의 한 점에 모여있기도 합니다. 다르게 표현하면 데이터가 흩어져 있다는 것은 분산이 크다는 것이고, 한 점에 모여있다는 것은 분산이 작다는 것입니다. 차원 축소의 목적은 차원을 줄이되, 최대한 정보의 손실을 줄이는 것입니다. 위 그래프에서 세 번째 축의 경우 모든 데이터가 거의 한 점에 모여 굉장히 많은 정보가 손실되었습니다. 즉, 분산을 가장 크게 하는 축을 찾아서 그 축으로 투영하면 정보의 손실을 최소화하면서 차원을 줄일 수 있습니다. 이것이 PCA의 핵심 아이디어입니다.

작동 방식

분산을 최대화하는 축을 찾는다는 것을 다르게 말하면 원본 데이터셋과 투영된 데이터셋 사이의 평균 제곱 오차(MSE)를 최소화하는 것입니다. 이렇게 첫 축을 찾았으면 다음으로 이 축과 직교하고 분산을 최대화하는 두 번째 축을 찾습니다. 다음 축은 두 축과 모두 직교하면서 분산을 최대화하는 축을 찾습니다. 이 과정을 반복해서 원하는 차원만큼 축을 찾습니다. 이때 각 축을 주성분(principal component, PC)라고 합니다.

그럼 주성분을 어떻게 구할 수 있을까요? PCA의 주성분은 교윳값 분해(eigendecomposition) 또는 SVD(특이값 분해)로 구할 수 있습니다. 교윳값 분해는 square matrix에 대해서만 정의되므로, 일반적으로 SVD를 사용합니다. SVD를 적용하면 훈련 데이터가 담긴 행렬 \( X \)를 \( U\Sigma V^T \)로 분해할 수 있습니다. 여기서 찾고자 하는 주성분의 단위 벡터가 \( V \)의 열에 담겨 있습니다.

\[ \mathbf{V} = \begin{pmatrix} \big| & \big| & & \big| \\ \mathbf{c}_1 & \mathbf{c}_2 & \cdots & \mathbf{c}_n \\ \big| & \big| & & \big| \end{pmatrix} \]

import numpy as np

X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt[0]
c2 = Vt[1]
print(c1, c2)
# [0.67857588 0.70073508 0.22023881] [-0.72817329  0.6811147   0.07646185]

이제 주성분을 모두 추출했습니다. \( d \)차원으로 줄이기 위해 처음 \( d \)개의 주성분으로 정의되는 초평면에 원본 데이터셋을 투영시킵니다. \( V \)의 첫 \( d \)열을 담은 행렬을 \( W_d \)라고 했을때,

\[ X_{d\text{-proj}} = X W_d \]

파이썬 코드에서는 \( d=2 \)로 줄여보겠습니다.


W2 = Vt[:2].T
X2D = X_centered @ W2

X2D.shape # (60, 2)

또는 편하게 사이킷런의 PCA 클래스를 사용하면 동일한 작업을 수행할 수 있습니다.

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X2D = pca.fit_transform(X)

자동 차원 선택

그런데 \( d \)를 얼마로 선택해야 할까요? 축소할 차원이 너무 낮으면 정보가 많이 손실됩니다. 사이킷런의 PCA 클래스에는 원래 분산의 특정 비율까지 차원을 줄이도록 설정할 수 있습니다. 위 코드에선 n_components에 \( d \)를 넣어 축소될 차원을 지정했지만, 0과 1 사이의 실수를 넣으면 원래 데이터의 해당 비율만큼의 분산을 유지하도록 하는 차원으로 축소합니다. 위 데이터는 원래 차원이 많지 않으니 MNIST 데이터셋을 사용해 보겠습니다. MNIST는 28x28 픽셀의 흑백 이미지로 이루어진 손글씨 숫자 데이터셋입니다. 즉, 각 이미지는 784개의 0~255 픽셀 값으로 표현됩니다. 보통 손글씨의 가장자리는 아무것도 적혀 있지 않고(0) 이웃한 픽셀 끼리는 비슷한 색인 경우가 많습니다. 원래 분산의 95%를 유지하면서 차원을 축소해 보겠습니다.

from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', as_frame=False)
X_train, y_train = mnist.data[:60000], mnist.target[:60000]
X_test, y_test = mnist.data[60000:], mnist.target[60000:]

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)

pca.n_components_ # 154

무려 784차원이던 데이터를 154차원으로 줄였습니다. 그럼에도 95%의 분산을 유지하고 있습니다. 이렇게 차원이 축소된 데이터를 다른 모델에 넣어 학습하면 성능이 개선되는 경우가 많습니다.

데이터 복원

PCA는 다시 원래 데이터를 복원하는 것도 가능합니다. 다만 이미 어느정도 데이터가 손실되었기 때문에 원본과 다를 수 밖에 없습니다. 그래도 굉장히 좋은 압축률에 비해서 복원된 데이터는 꽤 유사합니다.

\[ X_\text{recovered} = X_{d\text{-proj}}W_d^T \]

X_recovered = pca.inverse_transform(X_reduced)

Restored Data

PCA의 한계

PCA 구현의 문제는 SVD를 위해 전체 데이터셋을 메모리에 올려야 한다는 점입니다. 메모리보다 데이터셋이 큰 경우 SVD를 구하기 힘듭니다. 그래서 점진적 PCA(incremental PCA, IPCA)가 개발되었습니다. IPCA는 훈련 세트를 미니배치로 나눈 뒤 하나씩 처리합니다.

from sklearn.decomposition import IncrementalPCA

n_batches = 100
inc_pca = IncrementalPCA(n_components=154)

for X_batch in np.array_split(X_train, n_batches):
    inc_pca.partial_fit(X_batch)

X_reduced = inc_pca.transform(X_train)

또, \( m \)개의 feature를 가진 \( n \)개의 샘플이 있는 데이터에서 SVD를 수행할 때 시간복잡도는 \( O(mn^2 + n^3) \)입니다. 즉, 샘플 수가 많으면 어마어마하게 느려집니다. 그래서 사이킷런은 \( m \)이나 \( n \)이 500보다 클 때 Random PCA라는 확률적 알고리즘을 사용해 주성분의 근삿값을 찾습니다. 이 경우 시간복잡도는 \( d \)개의 주성분을 찾을 때 \( O(md^2 + d^3) \)으로 빠르게 수행할 수 있습니다.

또, PCA의 근본적인 한계가 있습니다. PCA는 선형 변환(linear transformation)을 사용합니다. 즉, 비선형 구조를 가진 데이터에 대해서는 효과적으로 작동하지 않습니다. 예를 들어, 스위스 롤(swiss roll) 데이터셋은 PCA로 좋은 결과를 얻기 어렵습니다.

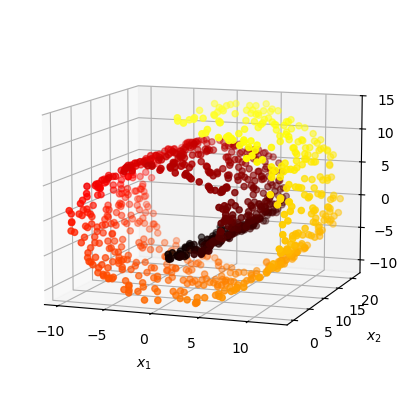
Swiss Roll

이런 경우에는 t-SNE나 UMAP 같은 비선형 차원 축소 기법을 사용해야 합니다.