벡터 함수
벡터 함수는 \( t \in \mathbb{R} \) 에 대해 벡터 \( \mathrm{r}(t) \)를 대응시키는 함수입니다.
\[ \mathrm{F}: \mathbb{R} \rightarrow \mathrm{V}_n \]
\[ t \longmapsto \mathrm{F}(t) = \left( f_1(t), f_2(t), \cdots, f_n(t) \right) \]
벡터 함수는 다음과 같은 성질을 가집니다.
\[ \left( \mathrm{F} \pm \mathrm{G} \right)(t) = \mathrm{F}(t) + \mathrm{G}(t) \]
\[ \left( \mathrm{F} \cdot \mathrm{G} \right)(t) = \mathrm{F}(t) \cdot \mathrm{G}(t) \]
\[ \left( \mathrm{F} \times \mathrm{G} \right)(t) = \mathrm{F}(t) \times \mathrm{G}(t) \]
벡터 함수의 미분
\( F \)를 아래와 같이 정의한다고 할때,
\[ \mathrm{F}(t) = \left( f_1(t), f_2(t), \cdots, f_n(t) \right) \]
\( t \)가 \( a \)로 갈 때의 극한은 각 함수 \( f_i \)의 극한과 같습니다.
\[ \lim_{t\rightarrow a} \mathrm{F}(t) = \left(\lim_{t\rightarrow a} f_1(t),\lim_{t\rightarrow a} f_2(t), \cdots,\lim_{t\rightarrow a} f_n(t) \right) \]
이를 이용하면 \( F' \)을 구할 수 있고 이를 접선벡터(tangent vector)라고 부릅니다.
\[ \mathrm{F}'(t) = \lim_{\Delta t \rightarrow 0} \frac{1}{\Delta t} \left( \mathrm{F}(t + \Delta t) - \mathrm{F}(t)\right) \]
\[ = \left( \lim_{\Delta t \rightarrow 0}\frac{f_1(t + \Delta t) - f_1(t)}{\Delta t}, \lim_{\Delta t \rightarrow 0}\frac{f_2(t + \Delta t) - f_2(t)}{\Delta t}, \cdots, \lim_{\Delta t \rightarrow 0}\frac{f_n(t + \Delta t) - f_n(t)}{\Delta t} \right) \]
\[ = \left( f_1'(t), f_2'(t), \cdots, f_n'(t) \right) \]
그리고 \( F \)와 \( F' \)는 서로 수직이라는 성질이 있습니다.
벡터함수에서 수직이라는 의미는 내적(inner product, dot product)의 값이 0이라는 의미입니다.
\[ \| \mathrm{F}(t) \|^2 = \mathrm{F}(t) \cdot \mathrm{F}(t) \]
양변을 미분하면
\[ 0 = 2\mathrm{F}'(t) \cdot \mathrm{F}(t) \]
이기 때문에 \( F \)와 \( F' \)의 내적이 0임을 알 수 있습니다.
매개화 (parameterization)
어떤 곡선 \( C \)를 다음과 같이 나타낼 때
\[ C = \{ r(t) \, | \, t \in [a, b] \} \]
\( r(t) \)가 곡선 \( C \)를 매개화한다고 합니다.
예제
\( y = x^2 \)을 매개화하여라.
\[ r(t) = ti + t^2j = (t, t^2) \]
또 다른 예시로 사이클로이드를 매개화해 표현하면
\[ r(t) = (t - \sin t)i + (1 - \cos t)j \]
입니다.
곡선의 길이
3D에서 \( r(t) = x(t)i + y(t)j + z(t)k \) 라고 하면 그때의 곡선의 길이는
\[ L = \int_a^b \sqrt{x'(x)^2 + y'(t)^2 + z'(t)^2} \,\, dt \]
\[ = \int_a^b \| r'(t) \| \, dt \]
임을 알 수 있습니다.
곡률 (Curvature)
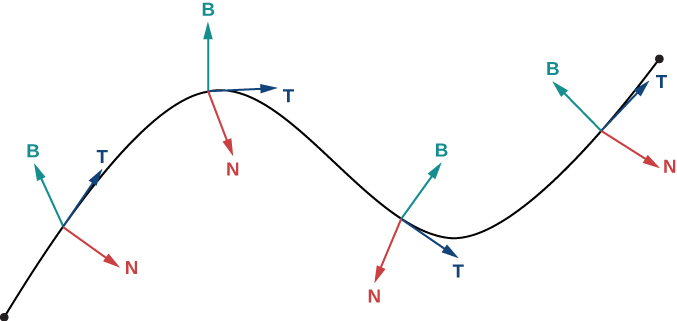
곡선 \( C = r(t) \)에서 \( r'(t) \)를 접선벡터라고 한다고 했습니다. 이때 단위접선벡터(unit tangent vector)는
\[ T(t) = \frac{r'(t)}{\|r'(t)\|} \]
이고 \( T'(t) \neq 0 \)인 \( t \)에 대해 법선벡터(normal vector)는
\[ N(t) = \frac{T'(t)}{\|T'(t)\|} \]
입니다. 3차원에서 곡선을 다룰 때는 접선벡터와 법선벡터만을 가지고는 정확하게 방향을 표현할 수 없습니다. 축이 3개이기 때문에 최소 3개의 벡터로 표현해야 합니다. 마지막 벡터는 접선벡터와 법선벡터에 동시에 수직이어야 하니 두 벡터의 외적(outer product, cross product)로 구할 수 있겠습니다. 이를 종법벡터(binormal vector)라고 합니다.
\[ B(t) = T(t) \times N(t) \]
이때 곡선이 휘어진 정도를 곡률(curvature)라고 합니다. 어떤 지점에 완벽히 접하는 반지름이 \( r \)인 원이 있을 때 그때의 곡률은 \( \frac{1}{r} \)입니다.
\[ \kappa(t) = \frac{\|T'(t)\|}{\|r'(t)\|} \]
곡률을 구하기 위해 생각보다 많은 과정을 거처야 해서 번거롭습니다. 근데 \( T(t) \)는 \( r(t) \)에서 파생되었으니 어떤 관계가 있을거라 추측할 수 있습니다. 아까 곡선의 길이를 구하는 식에서부터 시작해 보겠습니다.
\[ s = \int_a^t \|r'(u) \| du \]
\[ \frac{ds}{du} = \|r'(t) \| \]
다시 곡률로 돌아와 보면 (수식의 간결함을 위해 \( F(t) \)를 \( F \)로만 적겠습니다)
\[ T = \frac{r}{|r'|}, \,\,\, r' = |r'|T = \frac{ds}{dt}T \]
이 식에서 양변을 미분하면
\[ r'' = \frac{d^2s}{dt^2}T + \frac{ds}{dt}T' \]
\( T \times T = 0 \) 임을 이용해서
\[ r' \times r'' = \frac{ds}{dt}T \times \frac{d^2s}{dt^2}T + \frac{ds}{dt}T \times \frac{ds}{dt}T' \]
\[ = \left( \frac{ds}{dt} \right)^2\left( T\times T' \right) \]
\[ = \left( \frac{ds}{dt} \right)^2 |T||T'| \sin {\frac{\pi}{2}} \]
여기서 \( T \)는 단위벡터 였으니 norm이 1입니다.
\[ = \left( \frac{ds}{dt} \right)^2 |T| \]
따라서 식을 정리하면
\[ |T| = \frac{|r' \times r''|}{\left( \frac{ds}{dt} \right)^2} = \frac{|r' \times r''|}{|r'|^2} \]
이 되고 이 식을 다시 곡률에 대입하면
\[ \kappa(t) \frac{\|r'(t) \times r''(t) \|}{\|r'(t)\|^3} \]
임을 알 수 있습니다.