BFS (Breadth-First Search)

너비 우선 탐색(BFS)은 그래프 탐색(graph traversal) 알고리즘 중 하나로, 그래프의 모든 정점을 탐색하는 방법입니다. 그래프를 탐색하는 알고리즘은 굉장히 다양하게 있습니다. 그 중 BFS는 이름처럼 너비를 우선으로 탐색하는 방법입니다. 너비 우선이라는 말이 좀 어색한데, 쉽게 말해 가장 가까운(인접한) 노드부터 탐색하는 방법입니다. 아래 그림과 같은 그래프가 있다고 해 봅시다.

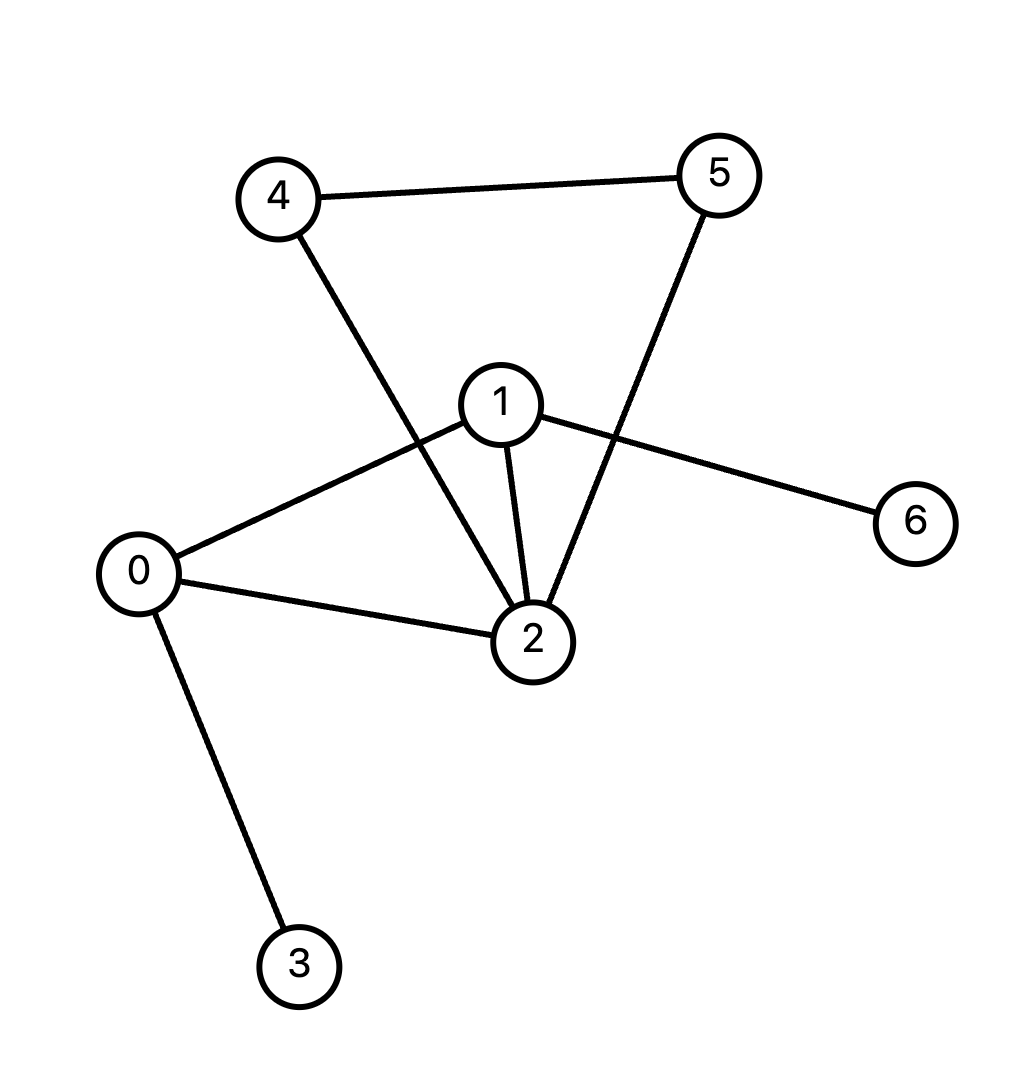
이 비방향 그래프를 0번 노드부터 시작해서 너비 우선 탐색을 진행합니다. 우선 0번 노드를 탐색합니다. 탐색이 완료된 노드는 완료 표시를 해서 다시 방문하는 일이 없도록 합니다.

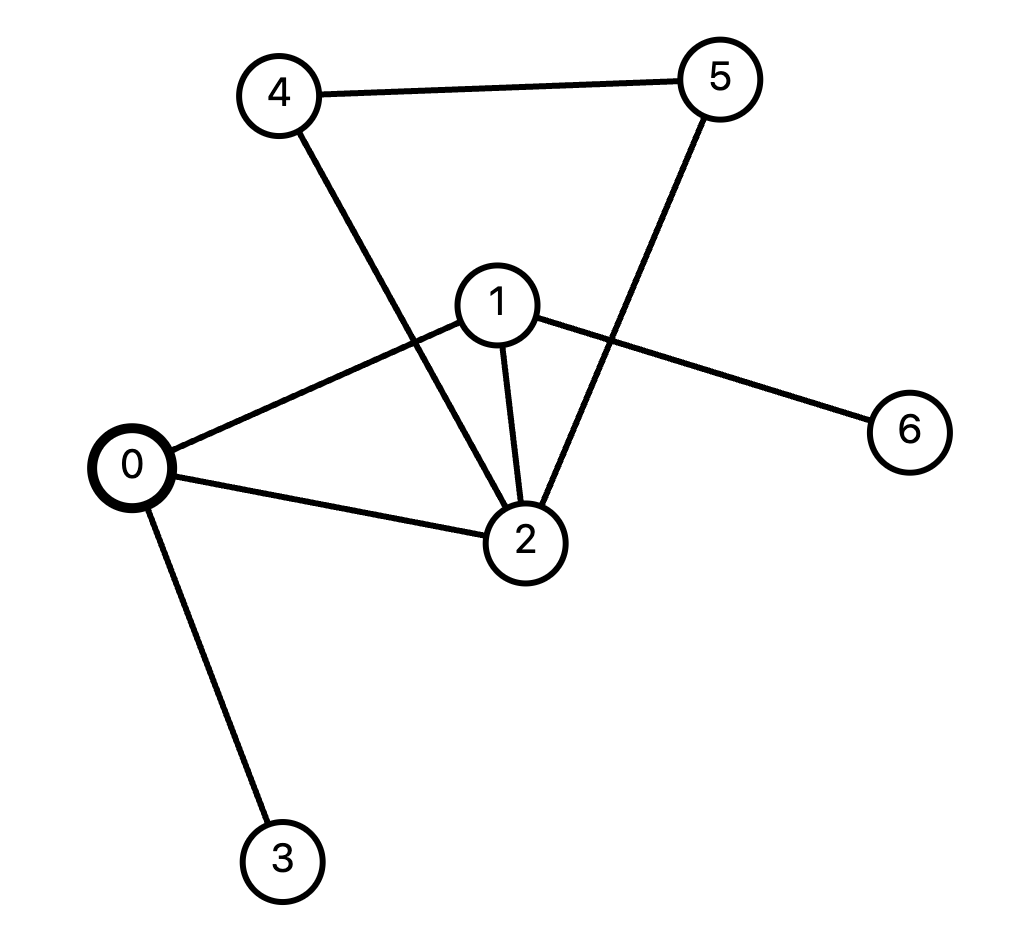
0번 노드와 연결된 노드는 1, 2, 3번 노드입니다. 너비 우선 탐색은 가장 가까운 노드부터 탐색하기 때문에 1, 2, 3번 노드를 탐색할 예정입니다. 이때 이 앞으로 탐색할 노드들의 계획을 저장하기 위해 큐(queue)를 사용합니다. 큐에 1, 2, 3을 넣고 1, 2, 3번 모두 방문 처리를 합니다. 아직 실제로는 방문하지 않았지만 큐에 들어가서 미래에 탐색될 예정이니 중복 탐색하지 않도록 처리를 해 줍니다.

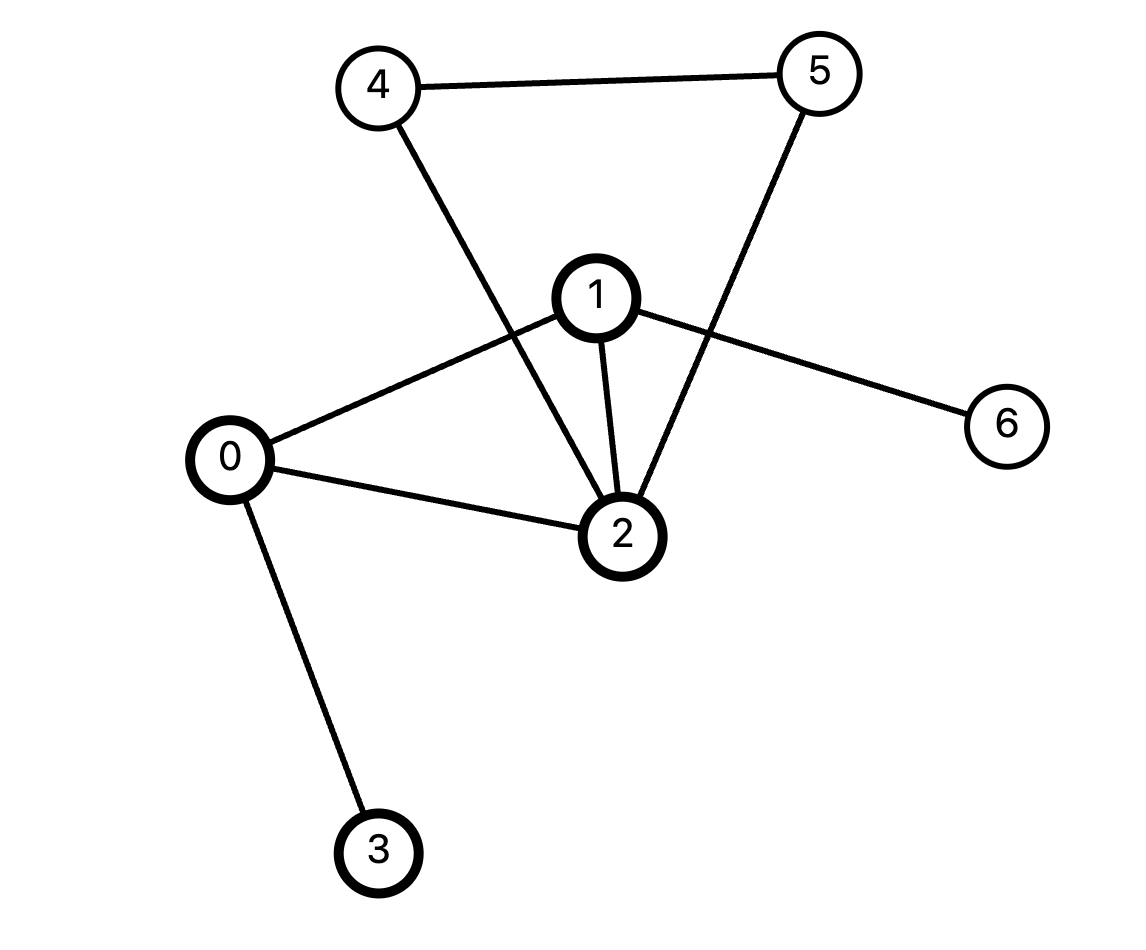
큐에서 노드 하나를 꺼냅니다. 1번 노드가 나왔으니 1번 노드를 탐색합니다. 1번 노드의 근처에는 0, 2, 6번 노드가 있습니다. 0번과 2번은 이미 방문 처리가 되어 있으니 6번 노드만 큐에 넣고 방문 처리를 합니다. 현재 큐에는 2, 3, 6번 노드가 있습니다.

이 과정을 큐가 빌 때까지 반복하다 보면 연결된 모든 노드를 탐색할 수 있습니다. 이것을 BFS라고 부릅니다. 코드로 옮겨 봅시다. 입력이 다음과 같이 주어집니다.

입력

첫 번째 줄에 노드의 개수 \( N \)과 간선의 개수 \( M \)이 주어집니다. 두 번째 줄부터 \( M \)개의 줄에 각각의 간선이 주어집니다. 간선은 두 개의 정수 \( u, v \)로 주어지며, \( u \)와 \( v \)는 연결되어 있습니다. 노드는 0부터 \( N - 1 \)까지의 정수로 표현됩니다. 그래프는 무방향 그래프입니다.

int main() {
    int n, m;
    cin >> n >> m;
    vector<int> adj[n];

    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    vector<bool> visited(n, false);
    queue<int> q;
    q.push(0); visited[0] = true;

    while (!q.empty()) {
        int node = q.front();
        q.pop();
        cout << node << " ";

        for (int neighbor : adj[node]) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }
}

격자 BFS

지금까지 저희는 연결된 일반적인 그래프에 대해서 BFS를 진행했습니다. 이런 형태의 그래프보다 더 자주 보이고 BFS를 적용하기 좋은 곳이 바로 격자입니다. 격자는 특별한 말이 없으면 상하좌우로 연결된 그래프입니다. 간선에 대한 정보가 없어도 좌표만 알고 있다면 인접한 노드가 어디인지 알 수 있습니다. 예를 들어, 포토샵에서 페인트통을 사용해서 색을 칠하는 것과 비슷합니다. 캔버스는 픽셀로 이루어진 2D 격자이고, 특정 픽셀에서 시작해서 상하좌우로 연결된 픽셀을 탐색해 같은 색으로 칠하는 것입니다. 격자에서 널리 사용되는 중요한 테크닉이 있습니다. 주변 노드를 나타내기 위해 dx, dy 배열을 사용하는 것입니다. 무슨 소리인가 하면,

int dx[4] = { 0, 0, -1, 1 };
int dy[4] = { -1, 1, 0, 0 };

이렇게 dx, dy배열을 만들어 놓고, 현재 노드의 좌표를 \( (x, y) \)라고 하면 인접한 노드의 위치를 dx, dy를 사용해서 구할 수 있습니다.

for (int i = 0; i < 4; i++) {
    int nx = x + dx[i];
    int ny = y + dy[i];
    // nx, ny가 격자 안에 있는지 확인
}

1926번: 그림

1926번: 그림 문제를 풀어 보겠습니다. \( n \times m \) 크기의 격자에서 1로 이루어진 그림 중 가장 큰 그림의 넓이를 구하는 문제입니다. 어느 한 지점에서 시작해서 상하좌우로 연결된 1 덩어리의 크기를 세면 됩니다. 똑같은 그림을 여러 번 세지 않도록 방문 처리에 주의해야 합니다.

#include <bits/stdc++.h>

using namespace std;
void fio() { cin.tie(nullptr); cout.tie(nullptr); ios::sync_with_stdio(false); }

int n, m;
int graph[500][500];
bool visited[500][500];
int dx[4] = { 1, -1, 0, 0 };
int dy[4] = { 0, 0, 1, -1 };

int bfs(int a, int b) {
    if (visited[a][b]) return 0;

    queue<pair<int, int>> q;
    q.push({a, b});
    visited[a][b] = true;

    int cnt = 0;
    while (!q.empty()) {
        auto [x, y] = q.front();
        q.pop();
        cnt++;

        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i];
            int ny = y + dy[i];

            if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
            if (visited[nx][ny]) continue;
            if (graph[nx][ny] != 1) continue;

            visited[nx][ny] = true;
            q.push({nx, ny});
        }
    }

    return cnt;
}

int main() {
    fio();

    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> graph[i][j];

    int ans = 0;
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (!visited[i][j] && graph[i][j] == 1) {
                int tmp = bfs(i, j);
                if (tmp > 0) {
                    cnt++;
                    ans = max(ans, tmp);
                }
            }
        }
    }

    cout << cnt << '\n';
    cout << ans << '\n';
}

본문에서는 해설하지 않았지만 BFS를 사용하면 한정적인 경우에 최단 경로를 찾을 수 있습니다. 앞으로 최단 경로 알고리즘에 대해서도 자세히 설명할 예정이지만, 만약 모든 간선의 가중치(길이)가 1이라면 BFS를 사용해도 최단 경로를 찾을 수 있습니다. 예제에 넣어놨으니 한 번 확인해 보세요.

BFS

BFS (Breadth-First Search)

격자 BFS

1926번: 그림

연습 문제