Sieve of Eratosthenes

에라토스테네스의 체는 특정 범위에서 소수 판별을 빠르게 하는 알고리즘입니다. 정확히는 많은 소수 판별을 빠르게 합니다. 에라토스테네스의 체는 1부터 \( N \)까지의 소수를 모두 찾는 알고리즘으로 고대 그리스의 수학자 에라토스테네스가 고안했습니다. 체로 거르듯이 소수가 아닌 수를 거르는 방식으로 동작합니다. 한번에 많은 수의 소수 판별이 필요할 때 유용하게 사용할 수 있습니다. 대신 많은 수에 대해서 여러 번 소수 판별이 필요한 것이 아니라면 에라토스테네스의 체가 더 느리게 작동할 수 있습니다.

소수 판별

소수 판별은 어떤 자연수 \( N \)에 대해서 \( N \)이 소수인지 아닌지를 판별하는 문제입니다. 자연수 \( N \)이 있을 때 2부터 \( N \)까지 반복하면서 나누어지는지 확인하고 나누어지지 않는다면 소수입니다. 조금 더 효율적으로 만들기 위해 \( \sqrt N \) 까지만 반복해도 작동합니다. 따라서 \( O(\sqrt N) \)짜리 알고리즘을 만들 수 있습니다.

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n;
    cin >> n;

    bool isPrime = true;

    if (n <= 1) isPrime = false;
    else if (n == 2) isPrime = true;
    else if (n % 2 == 0) isPrime = false;

    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            isPrime = false;
            break;
        }
    }

    if (isPrime) cout << "Prime";
    else cout << "Not prime";
}

2가 아닌 짝수는 소수가 아니기 때문에 2로 나누어 떨어지는지 확인하고 홀수인 경우에만 반복하도록 했습니다. 이렇게 하면 절반은 \( O(1) \)에 끝나기는 하지만 홀수 입력에서는 여전히 \( O(\sqrt N) \)입니다. 그런데 만약 이런 수가 \( M \)개 주어진다고 생각해 봅시다. 그러면 시간복잡도는 \( O(M\sqrt N) \)가 되고 \( M, N \)이 크면 시간초과(TLE)를 받게 됩니다. 이런 경우가 에라토스테네스의 체를 쓰기 좋은 경우입니다.

에라토스테네스의 체

1929번: 소수 구하기 문제를 봅시다. 1,000,000 이하의 양의 정수 \( N, M \)이 주어지고 \( [N, M] \) 범위에서 소수를 전부 찾는 문제입니다. 위에서 살펴본 방법대로 풀면 \( O(M \sqrt{M}) \)의 시간복잡도가 됩니다.

시간복잡도만 계산해 봤을 때는 10억이 되어 시간초과가 날 것 같지만, 생각보다 \( \sqrt{n} \)까지 반복되는 경우가 적기 때문에 아슬아슬하게 시간제한을 맞출 수 있습니다.

에라토스테네스의 체를 이용해서 풀어보도록 합시다. 에라토스테네스의 체의 기본 원리는 1부터 \( M \)까지 소수인지 저장하는 배열을 만들고 어떤 수가 소수인지 미리 처리해 두는 것입니다. sieve[n] 배열이 n이 소수인지 아닌지를 판별하는 bool 배열이라고 생각해 봅시다. sieve를 올바르게 만들었다면 다음부턴 \( O(1) \)에 소수인지 찾을 수 있습니다.

그렇다면 저 sieve 배열을 어떻게 만들어야 할까요? 예시로 1부터 100까지(길이가 101인) true로 저장된 배열이 있습니다. 1은 소수가 아니니 false로 처리해둡니다.

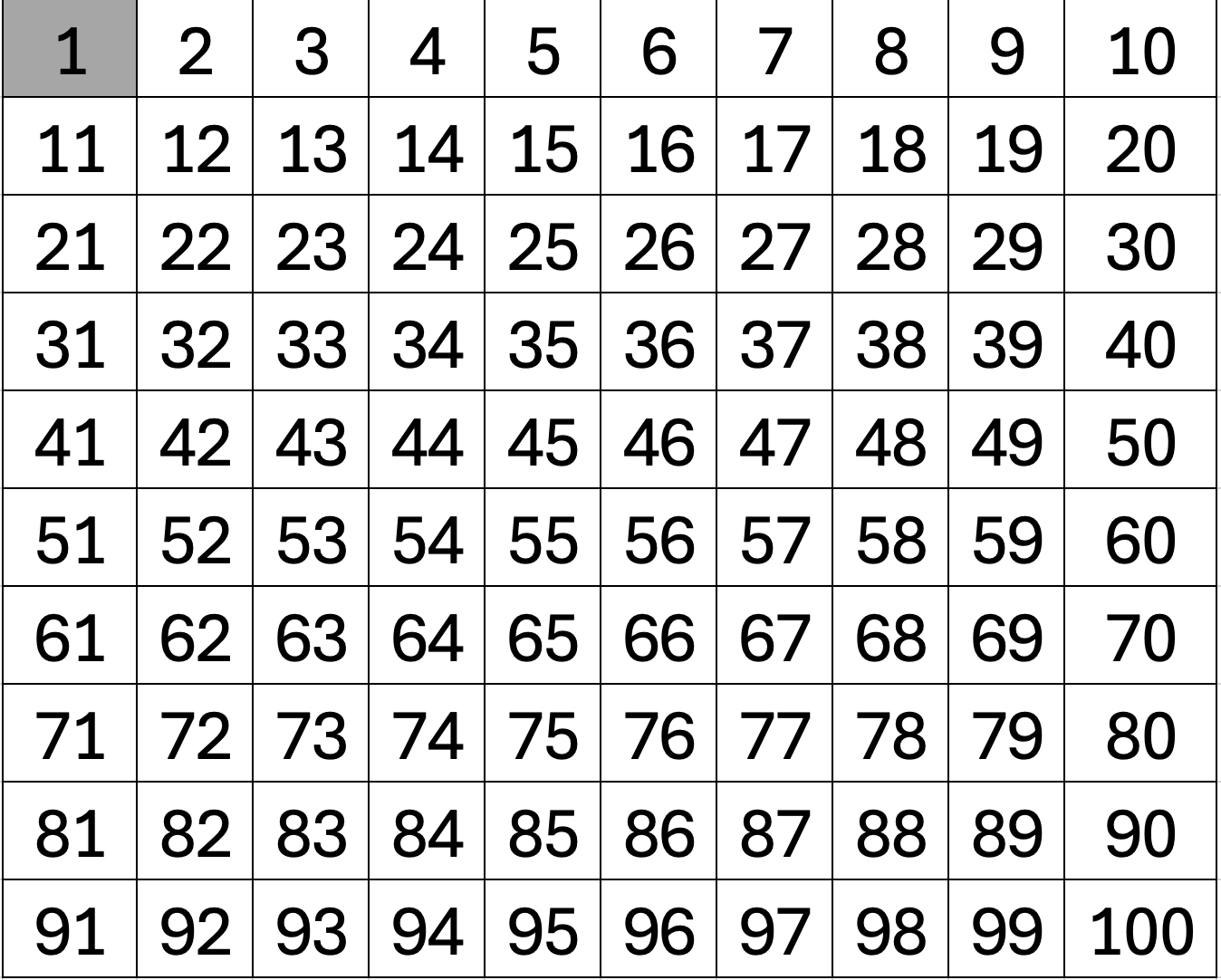
이제 2부터 시작해서 하나씩 증가시키며 반복합니다. sieve가 true라면 그 수가 소수라는 의미입니다. 그런데 어떤 수 \( k \)가 소수이면 그 수의 배수 \( rk \,\, (r \geq 2) \)는 소수가 아니므로 false로 처리합니다.

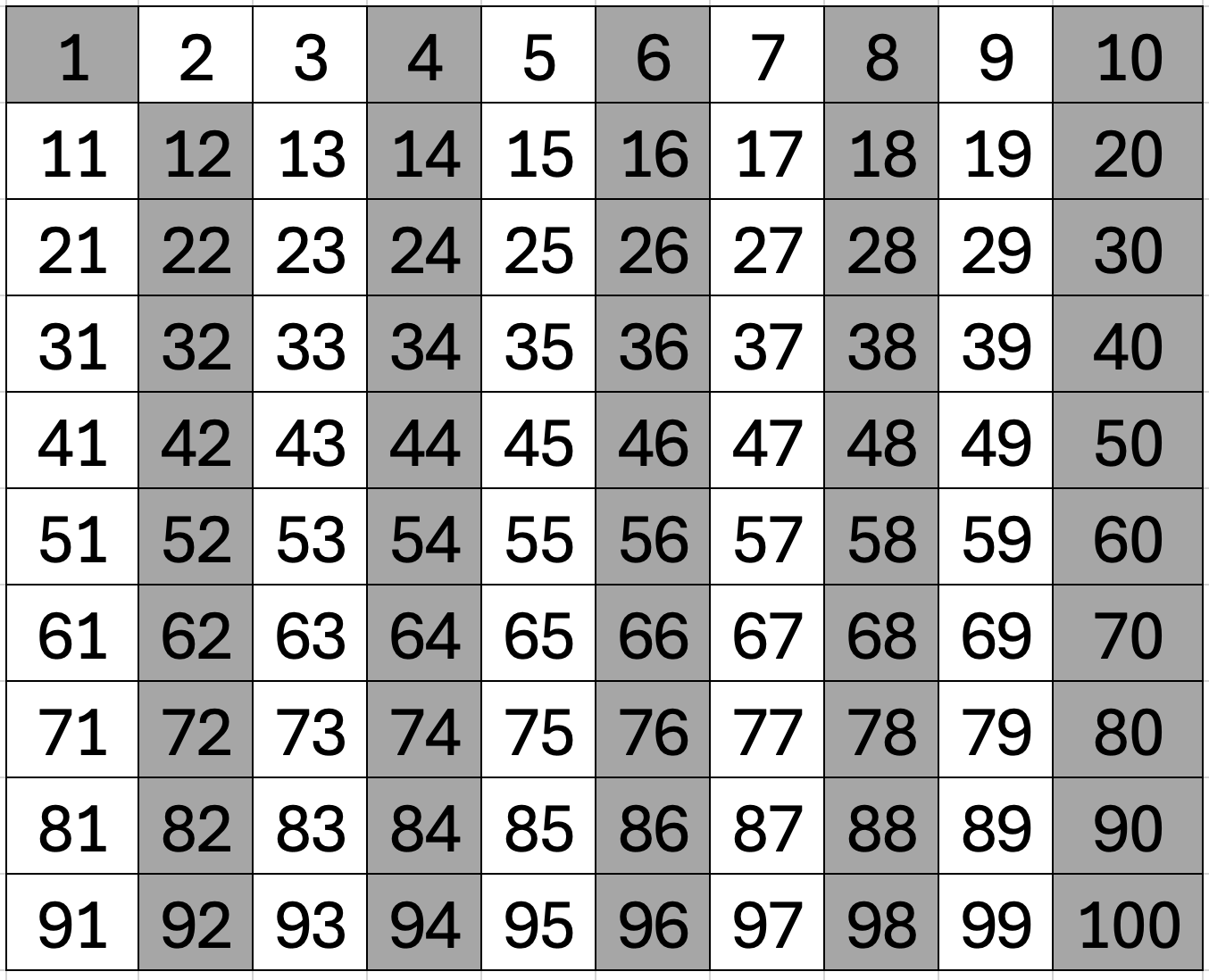
다음 수는 3입니다. 3이 true니까 3은 소수고 3의 배수는 소수가 아닙니다. 다시 false로 체크합니다.

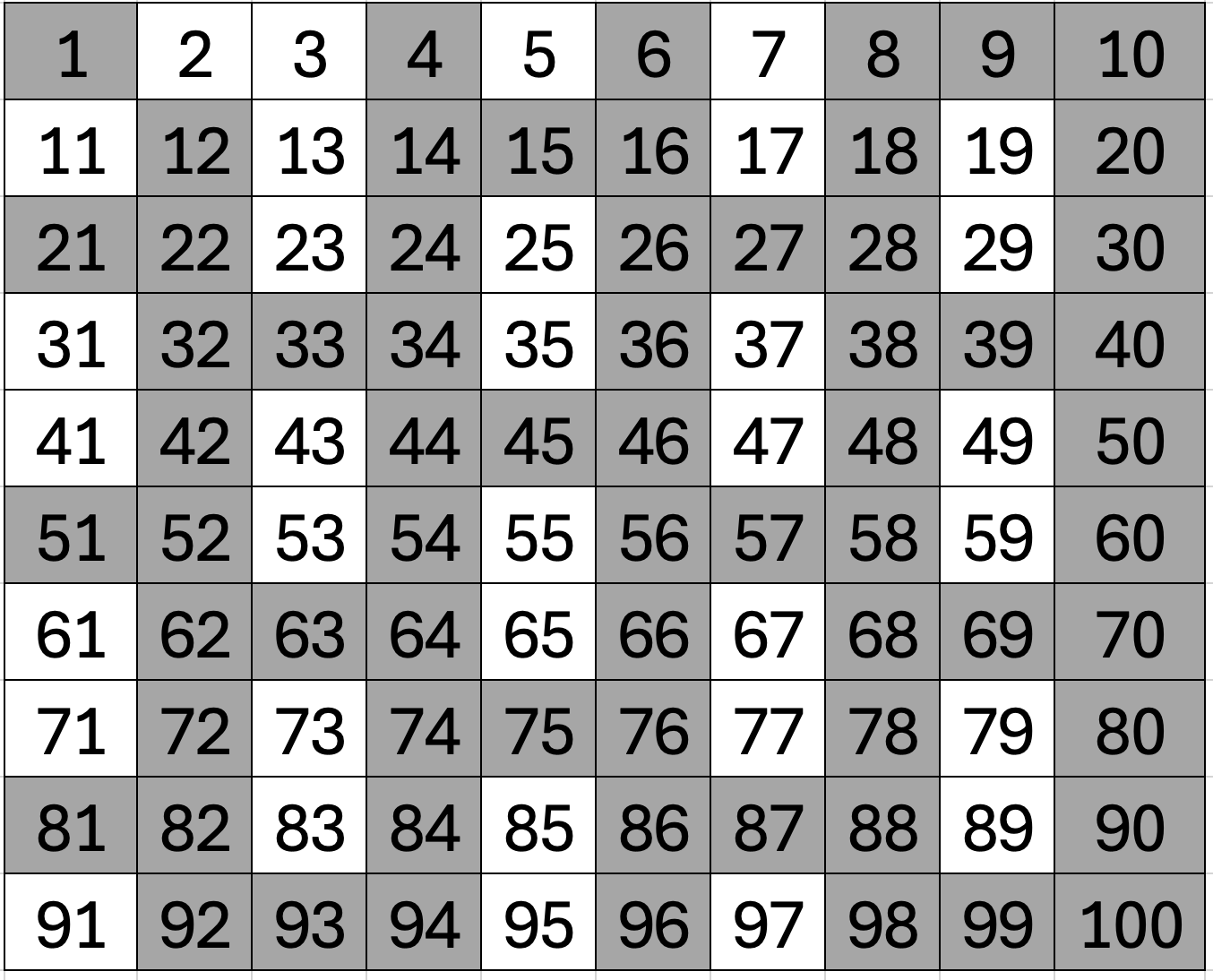
다음 수는 4이지만 false로 표시되어 있습니다. 따라서 소수가 아닙니다. 그래서 스킵하고 다음 true인 5로 찾아갑니다. 5는 true로 되어 있으니 소수이고 5의 배수를 false로 표시해 줍니다. 다음엔 7의 배수, 11의 배수, 13의 배수 ... 이렇게 쭉 반복합니다. 직접 해 보면 알겠지만 7의 배수까지만 표기해도 더이상 새롭게 false가 되는 수가 없습니다. 완성된 모습은 다음과 같습니다.

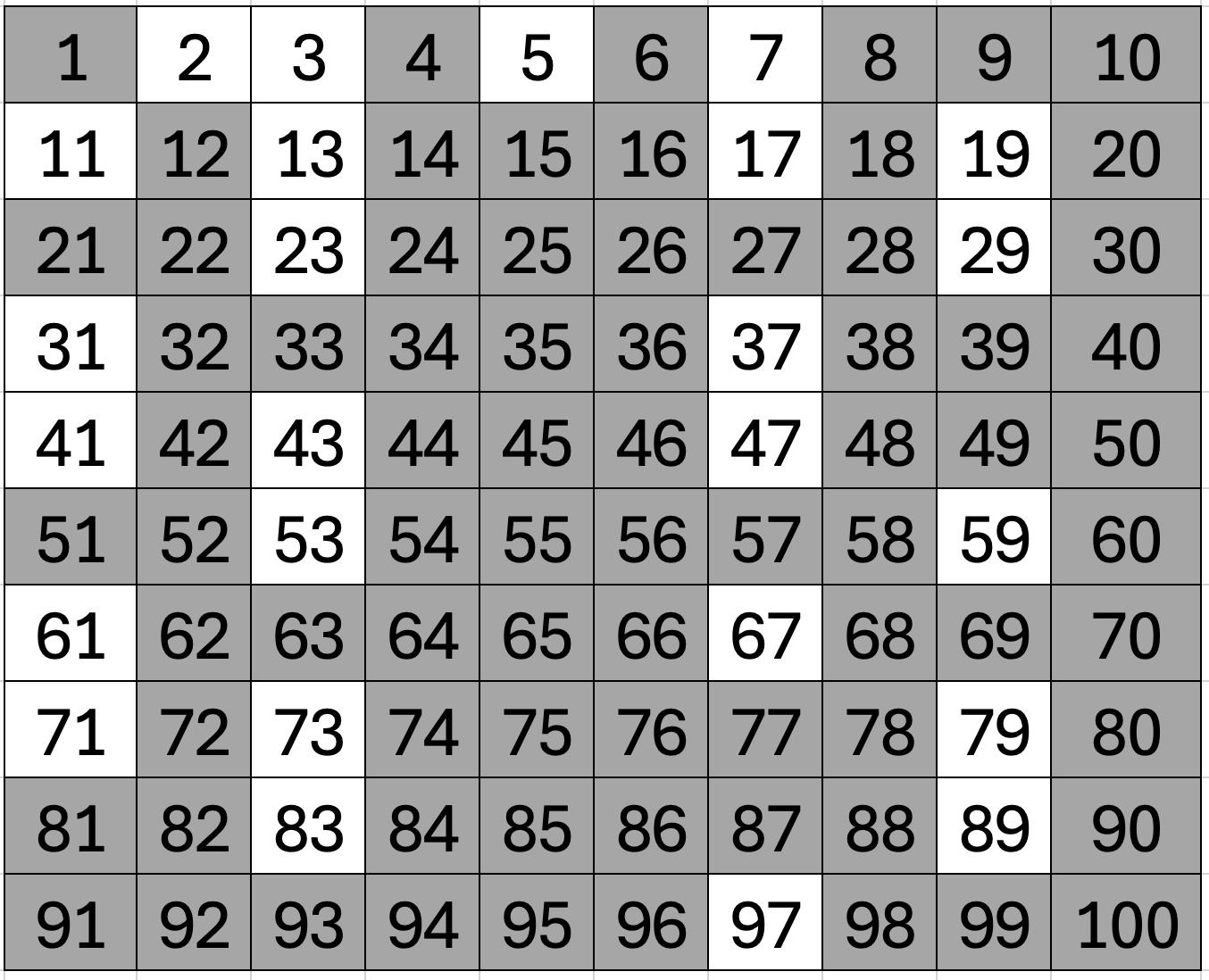
따라서 true로 표시되어 있는 2, 3, 5, 7 ... 97 까지 25개의 수가 소수임을 알 수 있습니다. 실제로는 bool sieve[101]을 가지고 있을 것이고 sieve[83] 처럼 바로 소수인지 알 수 있습니다. 여기까지 코드로 만들어 보겠습니다.

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n = 100;
    bool sieve[n + 1];
    fill(sieve, sieve + n + 1, true);
    sieve[0] = sieve[1] = false;
    
    for (int i = 2; i <= n; i++)
        if (sieve[i])
            for (int j = 2 * i; j <= n; j += i)
                sieve[j] = false;
}

이 코드의 시간복잡도는 각 루프마다 \( \frac{N}{i} \)번 반복하므로 \( \sum\frac{N}{i} \approx N \log N \) 따라서 \( O(N \log N) \)의 시간복잡도를 갖습니다.

최적화

여기서 조금 더 시간복잡도를 줄일 수 있습니다. 위에서 직접 손으로 색칠했을 때 생각보다 중복되는 반복이 굉장히 많습니다. 위 코드에서 \( j \)가 \( 2i \)부터 시작했는데 사실 \( i^2 \) 부터 시작해도 동일한 결과를 얻습니다. 왜 이렇게 되는지는 아래에 증명해 두었습니다.

증명

모든 합성수는 두 수의 곱으로 나타낼 수 있다. 즉 합성수 \( c \)는 \( c = ab \)이다. 이때 \( a, b \)중 최소 하나는 \( \sqrt c \)보다 작아야 한다. 둘 다 \( \sqrt c \)보다 크다면 \( ab \)가 \( c \)보다 커지기 때문이다. 어떤 소수 \( i \)에 대해, 어떤 합성수 \( c = ib \)가 있다면 \( b \)는 \( \sqrt c \)보다 크거나 같다.

b가 i보다 작다면 이미 이전 반복에서 지나왔을 것이다.
j < i인 수 ji가 있었다면 이미 이전 반복에서 지워졌을 것이다.

따라서 \( i^2 \)부터 지워도 된다.

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n = 100;
    bool sieve[n + 1];
    fill(sieve, sieve + n + 1, true);
    sieve[0] = sieve[1] = false;

    for (int i = 2; i <= n; i++)
        if (sieve[i])
            for (int j = i * i; j <= n; j += i)
                sieve[j] = false;
}

그럼 이때의 시간복잡도는 \( O(N \log \log N) \)가 됩니다. 시간복잡도의 증명도 아래에 적어두겠습니다.

시간복잡도 증명

어떤 소수 \( p \)에 대해서 \( p^2, p(p + 1), \dots \)를 지우니 지우는 횟수는 \( \frac{n - p^2}{p} \approx \frac{n}{p} \)이다. 즉, 총 연산 횟수는

\[ \sum_\underset{p \text{ prime}}{p \leq n} \frac{n}{p} = n \sum_\underset{p \text{ prime}}{p \leq n} \frac{1}{p} \approx n \log \log n \]

이렇게 정리됩니다. 소수의 역수의 합은 자연로그의 로그와 근사하는 것으로 메르텐스의 제 2정리에 의해 알려져 있습니다. 자세한 증명에 대해서는 여기를 참고해 주세요.

Sieve of Eratosthenes