YEAHx4YEAHx4

Sort

정렬

YEAHx4

YEAHx4

2025-04-19
20 mins

Sort

정렬은 정말 널리 사용되는 알고리즘입니다. 정렬은 어떤 기준에 따라서 배열의 원소들을 나열하는 알고리즘입니다. 일반적으로 오름차순(ascending)과 내림차순(descending)을 가장 많이 사용하며 오름차순 정렬이 기본값으로 설정되어 있습니다. 정렬을 구현하는 정말 다양한 알고리즘이 있지만 결론부터 말하자면, 언어에서 제공되는 기본 정렬을 사용하는 것이 좋습니다. 왠만한 언어에서는 항상 빠름이 보장되는 정렬 알고리즘이 있고 한 줄이면 사용이 가능합니다. 그래서 대부분 직접 구현하지 않고 가져다 쓰는 것이 좋습니다.

Selection Sort

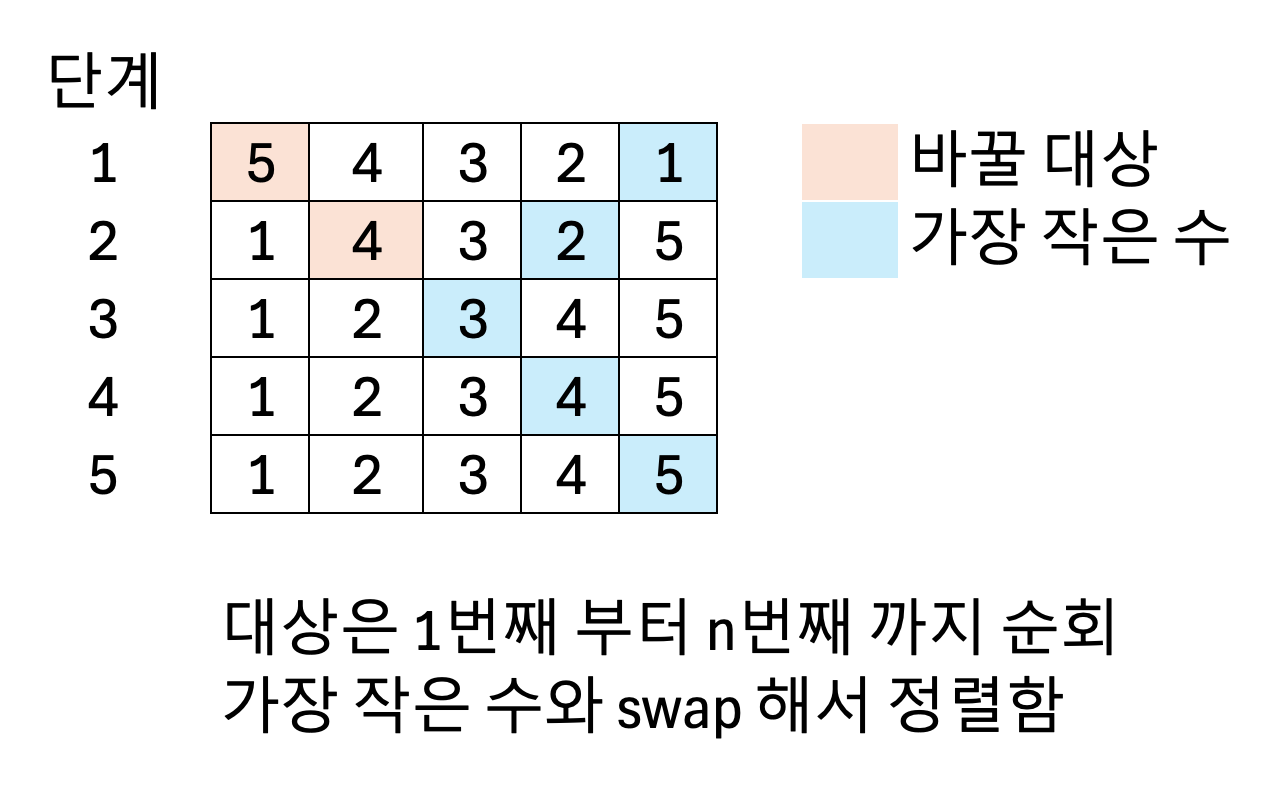
선택 정렬은 리스트에서 가장 작은 값을 찾아서 맨 앞에 가져다 놓는 방식입니다. \( i \)가 \( [0, \text{len}) \) 일 때, \( i \)의 뒤에서 가장 큰 값을 찾아서 \( i \)번째 수와 교환하는 방식입니다. 시간복잡도는 \( O(n^2) \) 이 됩니다.

Selection Sort 

#include <iostream>
using namespace std;

int main() {
    int a[] = { 5, 7, 2, 9, 1, 3, 8, 4, 6 };
    int n = sizeof(a) / sizeof(a[0]);

    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (a[j] < a[minIndex]) {
                minIndex = j;
            }
        }
        swap(a[i], a[minIndex]);
    }

    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }

    return 0;
}

구현이 굉장히 간단하지만 \( O(n^2) \)의 높은 시간복잡도를 갖습니다.

Bubble Sort

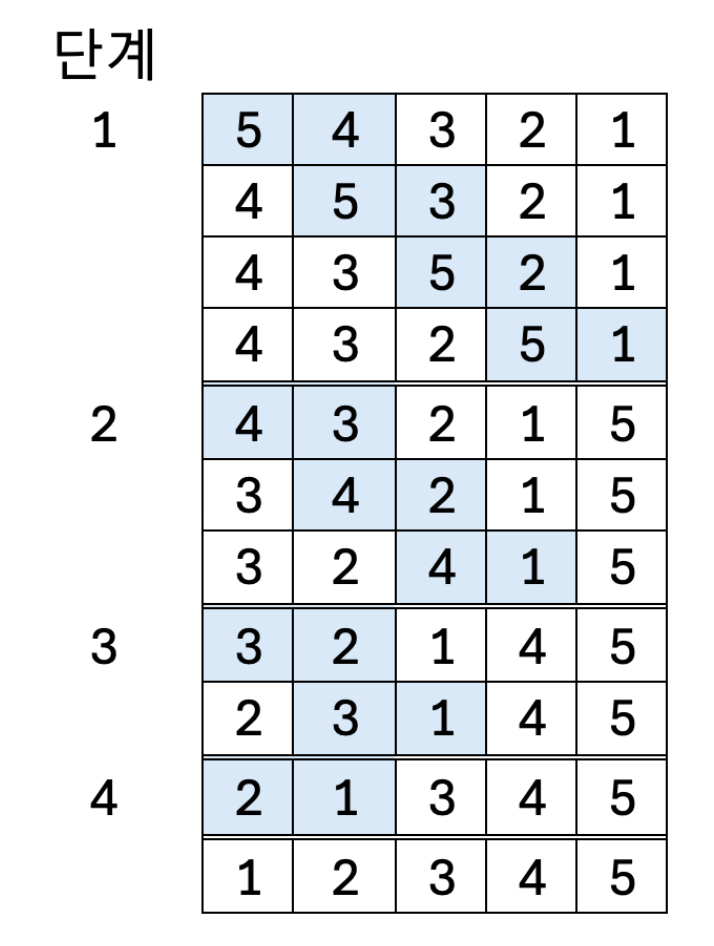
버블 정렬은 인접한 두 원소를 비교해서 작은 수가 앞으로 오도록 자리를 바꾸는 방식입니다. 이 과정을 \( n \)번 반복하면 배열의 원소가 정렬됩니다.

Bubble Sort 

#include <iostream>
using namespace std;

int main() {
    int a[] = { 5, 7, 2, 9, 1, 3, 8, 4, 6 };
    int n = sizeof(a) / sizeof(a[0]);

    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - 1 - i; j++) {
            if (a[j] > a[j + 1]) {
                swap(a[j], a[j + 1]);
            }
        }
    }

    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }

    return 0;
}

마찬가지로 구현은 간단하지만 \( O(n^2) \)의 시간복잡도를 갖습니다.

Quick Sort

퀵 정렬은 이름처럼 앞서 살펴본 정렬보다는 빠른 정렬입니다.

  1. 어떤 pivot(기준)을 정한다.
  2. pivot을 기준으로 작은 값들을 왼쪽, 큰 값들을 오른쪽으로 옮긴다. 즉, 리스트를 두 파티션으로 쪼갠다.
  3. 각 파티션에 대해서도 1, 2번 과정을 재귀적으로 반복한다. 더이상 나눌 수 없을 때까지 반복한다. 즉, 파티션의 크기가 0이나 1이 될 때까지 반복한다.
  4. 잘게 쪼개진 파티션을 다시 합치면 정렬이 완료된다.

여기서 피벗을 정하는 기준은 여러가지가 있는데, 어떤 걸로 하던 크게 상관은 없습니다. 대신 피벗에 따라 시간복잡도가 꽤 크게 차이날 수 있습니다. 예를 들어, 가장 작은 값이나 큰 값을 계속 피벗으로 선택한다면, 파티션이 제대로 나눠지지 않겠죠. 이론상 완벽하게 반씩 나눌 때 \( O(n \log n) \)의 시간복잡도를 갖게 되는데 계속 이상한 값을 피벗으로 선택하면 최악의 경우 \( O(n^2) \)이 될 수 있습니다. 일단 가운데 수를 피벗으로 삼는 경우를 생각해보겠습니다.

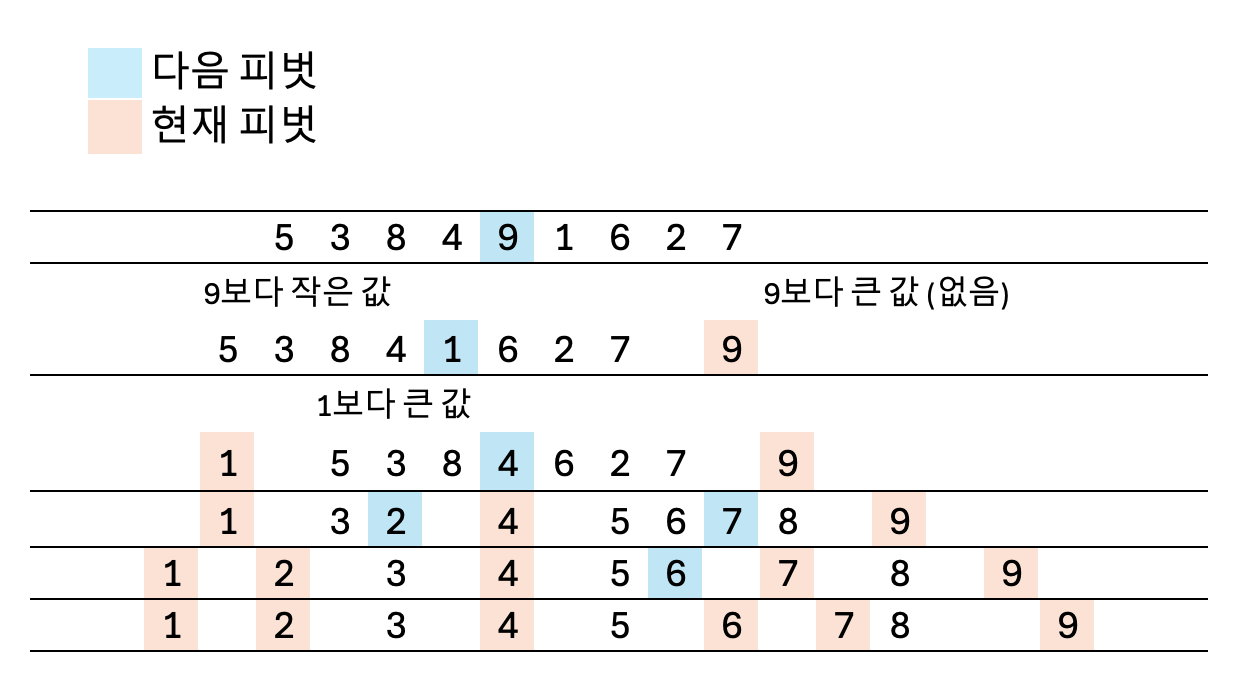
Quick Sort

이렇게 정렬이 진행됨을 알 수 있습니다. 재귀함수를 기반으로 작동하고 최적의 경우 배열을 반씩 줄여나가기 때문에 \( \log n \) 단계가 진행됩니다. 각 단계에서 \( n \)개의 원소를 순회하므로 시간복잡도는 \( O(n \log n) \)이 됨을 알 수 있습니다. 하지만, 위에서 얘기한대로 피벗을 계속 잘못 잡으면 위 그림의 1단계처럼 한 원소만 계속 떼어내기 때문에 \( O(n^2) \) 시간이 걸리게 됩니다. 그래서 피벗을 랜덤하게 잡는 등 여러가지 시도가 있습니다. 퀵 소트를 코드로 구현해봅시다.

#include <iostream>
using namespace std;

void quickSort(int a[], int left, int right) {
    if (left >= right) return;

    int pivot = a[(left + right) / 2];
    int i = left, j = right;

    while (i <= j) {
        while (a[i] < pivot) i++;
        while (a[j] > pivot) j--;
        if (i <= j) {
            swap(a[i], a[j]);
            i++; j--;
        }
    }

    quickSort(a, left, j);
    quickSort(a, i, right);
}

int main() {
    int a[] = { 5, 7, 2, 9, 1, 3, 8, 4, 6 };
    int n = sizeof(a) / sizeof(a[0]);

    quickSort(a, 0, n - 1);

    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }

    return 0;
}

STL

하지만, 앞서 언급한 대로 정렬 알고리즘을 직접 구현해서 사용하지 않습니다. 대부분의 현대 언어에서는 내장 정렬 알고리즘을 지원하기 때문입니다. 더구나 위의 퀵 정렬이 최악의 경우 \( \Theta(N^2) \)인 것에 반해 기본으로 제공되는 정렬은 quick, merge, heap 정렬 등을 상황에 맞게 사용하는 하이브리드 소트를 하기 때문에 모든 경우에서 \( O(n \log n) \)을 보장합니다. 그래서 대부분의 경우 직접 정렬을 구현하면 시간초과의 원인이 될 수 있습니다.

C++

C++에서는 algorithm 헤더의 sort 함수를 통해서 정렬을 수행할 수 있습니다.

int main() {
    int n; cin >> n;
    int a[n];
    for (int i = 0; i < n; i++) cin >> a[i];
    
    sort(a, a + n);
}

기본적으로 오름차순으로 정렬됩니다. 종종 내림차순이나 다른 정렬 기준으로, 또는 정수가 아닌 구조체를 정렬해야 하는 경우가 있습니다. 그럴 때 세 번째 인자로 bool을 리턴하는 함수를 넣어주면 원하는 기준에 따라서 정렬할 수 있습니다.

int main() {
    int n; cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++) cin >> a[i];

    sort(a.begin(), a.end(), greater<>());
}

Python

파이썬에서는 sorted나 sort로 정렬을 할 수 있습니다.

a = list(map(int, input().split()))
a = sorted(a)

파이썬에서 내림차순 정렬이 필요할 경우 reverse=True 옵션을 넣어서 결과를 뒤집을 수 있습니다. 만약 원하는 기준으로 정렬해야 한다면 key 옵션에 어떤 값을 반환하는 함수를 넣으면 그 값을 기준으로 오름차순 정렬을 진행합니다. 아래는 절댓값을 내림차순으로 정렬하는 코드입니다.

a = list(map(int, input().split()))
a.sort(reverse=True, key=lambda x: abs(x))

Stable Sort

안정 정렬(stable sort)는 우선순위가 같은 요소가 여러개일때 각 요소의 상대적인 순서가 유지되는 정렬을 의미합니다. 예를 들어 (1, 2), (1, 1) 이 들어 있고 첫번째 값을 기준으로 정렬한다고 했을 때 stable sort는 (1, 2), (1, 1) 처럼 원래 순서가 그대로 유지되지만 unstable sort에서는 그 순서를 보장하지 않습니다. 즉 매 상황마다 같은 수도 있고 다를 수도 있다는 뜻입니다. 파이썬에서는 Timsort라는 하이브리드 알고리즘을 사용하기 때문에 기본적으로 stable sort를 지원합니다. 하지만 C++에서는 속도를 위해 stable 하지 않습니다. 대신, stable\_sort 라는 함수가 따로 제공되어 대신 사용할 수 있도록 하고 있습니다.

Counting Sort

카운팅 정렬(계수 정렬)은 특수한 경우에 사용할 수 있는 \( O(N) \)으로 굉장히 빠른 알고리즘입니다. 예를 들어, 1억 개의 숫자를 정렬해야 하는데, 모든 숫자가 0이상 100이하의 정수라고 해 봅시다. 이런 경우 1억개의 숫자를 저장하기는 비효율적입니다. 범위가 100밖에 안되는데 숫자는 어마어마하게 많기 때문에 비둘기집 원리에 의해 많은 수가 서로 중복될 것이기 때문입니다. 이런 경우 counting sort가 굉장히 효율적입니다. 길이가 101인 배열을 만들어서 각 숫자가 몇개인지를 저장하면 다시 복원할 수 있습니다. 이것을 counting sort라고 합니다.

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    vector<int> count(101, 0);

    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        count[x]++;
    }

    for (int i = 0; i <= 100; i++) {
        while (count[i]--) {
            cout << i << " ";
        }
    }
    return 0;
}

마치며

정렬에 관해서 꽤 긴 글을 썼습니다. 정렬은 PS가 아니더라도 정말 자주 사용되는 알고리즘이니 확실히 알아두는 것이 좋습니다. 여기서 살펴본 정렬 알고리즘 말고도 merge sort, heap sort, radix sort 등 정말 다양한 알고리즘들이 있습니다. 특정한 조건 하에서 극한의 성능이 필요하다면 특수한 정렬 알고리즘을 직접 구현할 때가 있을 수도 있습니다. 여러 알고리즘들이 어떻게 정렬되는지 눈으로 보고 싶다면 유명한 이 영상을 추천합니다. 이 글이 많은 도움이 되었으면 좋겠습니다.

연습문제