분할 정복
분할 정복은 문제를 작은 서브 문제로 나누어 푸는 방법입니다. 대표적인 분할 정복의 예시로는 병합 정렬(merge sort), 퀵 정렬(quick sort), 이전 챕터에서 살펴본 거듭제곱을 구하는 방법이 있습니다. 분할 정복은 일반적으로 다음과 같은 세 단계로 이루어집니다.
- 분할: 문제를 작은 서브 문제로 나누는 단계입니다. 이때 서브 문제는 원래 문제와 비슷한 형태를 가지지만 훨씬 풀기 쉽습니다. 어느 순간 서브 문제의 크기가 작아져서 직접 풀 수 있는 단계에 도달합니다.
- 정복: 서브 문제를 해결하는 단계입니다. 충분히 분할을 했다면 서브 문제는 직접 풀 수 있습니다.
- 결합: 서브 문제의 해답을 결합하여 원래 문제의 해답을 구하는 단계입니다.
이전 챕터에서 살펴봤던 거듭제곱을 구하는 방법을 예로 들어보겠습니다. \( a^n \)을 구하고 싶은데 바로 구하기 너무 어렵습니다. 그래서 \( a^{n / 2} \)의 제곱으로 작은 문제로 나눕니다. 계속 나누다 보면 어느 순간 \( a^1 \)이 주어지고 이제는 직접 구할 수 있습니다. 이제 \( a^1 \)을 가지고 \( a^2 \), \( a^4 \), \( a^8 \)...을 구할 수 있습니다. 즉, 쉽게 답을 구할 수 있을 때까지 계속 분해하고 다시 결합해 원래 문제를 해결하는 것입니다.
1074번: Z
1074번: Z는 분할 정복을 이용한 대표적인 예시입니다. 실제로 시뮬레이션하면서 진행하면 시간복잡도는 \( O(4^n) \)이 되어 0.5초의 시간제한을 맞출 수 없습니다.
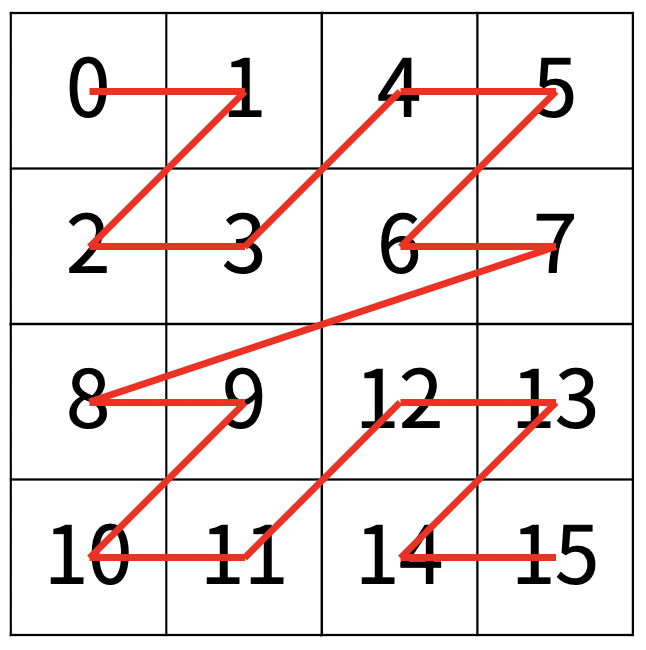
이 그림에서 입력으로 2행 0열이 주어지면 8을 출력하는 것이 목표입니다. 문제를 보면 알 수 있듯이 전체 배열을 4등분하여 왼쪽 위, 오른쪽 위, 왼쪽 아래, 오른쪽 아래 순서로 방문합니다. 여기서 우리가 알 수 있는 사실은 탐색하고 싶은 좌표가 어느 사분면에 속하는지 알 수 있다는 것입니다. 위 그림을 4등분하면 (2, 0)은 왼쪽 아래 사분면에 속합니다. 그러면 나머지 3개의 사분면은 탐색할 필요조차 없어집니다. 즉, 탐색할 좌표가 속하는 사분면을 찾고 그 사분면 안에서 다시 탐색을 계속 진행하다보면 \( 2 \times 2 \) 배열이 나올 때까지 계속 분할할 수 있습니다. 여기서 마지막으로 분할하면 \( 1 \times 1 \) 배열이 되니 원하는 좌표를 확정지을 수 있습니다. 이렇게 비슷한 문제가 반복되는 특성 덕분에 재귀로 자주 구현됩니다. 이제 코드로 옮기기만 하면 정답을 받을 수 있습니다. 생각보다 코드 만들기가 쉽지 않으니 직접 구현해보는 것을 추천합니다.
#include <iostream>
using namespace std;
int z(int n, int r, int c) {
if (n == 0) return 0;
int half = 1 << (n - 1);
int area = half * half;
if (r < half && c < half)
return z(n - 1, r, c);
else if (r < half && c >= half)
return area + z(n - 1, r, c - half);
else if (r >= half && c < half)
return 2 * area + z(n - 1, r - half, c);
else {
return 3 * area + z(n - 1, r - half, c - half);
}
int main() {
int n, r, c;
cin >> n >> r >> c;
cout << z(n, r, c) << '\n';
return 0;
}