시간복잡도
모든 문제는 제한시간이 있습니다. 예를 들어, 제한시간이 1초인 문제는 코드가 1초 안에 입력을 받고 결과를 출력해 종료되어야 합니다. 만약 제한시간을 초과하면 시간초과(TLE, Time Limit Exceeded) 판정을 받게 됩니다. 문제를 풀 때 코드를 작성하는 것은 꽤 시간이 걸리고 힘든 작업입니다. 그런데, 시간 초과를 받게 되면 애초에 접근이 잘못되었다는 의미입니다. 어떤 문제에 대해 여러가지 접근 방법을 떠올렸다고 해 봅시다. 코드를 직접 작성하지 않고도 각 방법이 시간이 얼마나 걸릴지 미리 예측할 수 있다면 좋지 않을까요?
시간복잡도는 어떤 알고리즘의 성능을 예측하는데 사용되는 중요한 지표입니다. 예를 들어 아래의 코드를 봅시다.
int n; cin >> n;
for (int i = 0; i < n; i++) {
// ...
}이 for문은 몇 번 반복될까요? 당연히 \( n \)번 입니다. 따라서 이 코드의 시간복잡도는 \( O(n) \)이라고 할 수 있습니다. 이렇게 대문자 O 안에 어떤 함수를 넣어 시간복잡도를 표기하는 것을 Big-O 표기법이라고 합니다. 표기법은 여러 가지가 있지만 주로 Big-O 표기법으로 표현합니다.
시간복잡도는 입력의 크기에 따른 알고리즘의 수행 시간을 나타냅니다. 위의 코드를 보면, 입력 \( n \)이 커질수록 for문이 반복되는 횟수도 증가합니다. 따라서 시간복잡도는 입력 크기 \( n \)에 대한 함수로 표현됩니다.
그렇다면 아래 코드의 시간복잡도는 얼마일까요?
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// ...
}
}\( n \)에 따른 반복 횟수를 계산해봅시다. \( i \)가 0이면 \( j \)는 1부터 \( n - 1 \)까지, \( i \)가 1이면 \( j \)는 2부터 \( n - 1 \)까지 반복됩니다. 계산을 편하게 하기 위해 뒤에서부터 생각해보면 \( 0 + 1 + \cdots +(n-1) \)인 것을 알 수 있습니다. 따라서 이것을 정리하면
그럼 이때의 시간복잡도는 \( O\left(\frac{n(n-1)}{2}\right) \)인 걸까요? 정답은 아닙니다. 시간복잡도의 목적은 입력에 따른 반복 횟수의 대략적인 추세를 보고 싶은 것이지 정확한 반복 횟수를 구하고 싶은 것이 아닙니다. 그리고 정확히 반복 횟수를 구할 수 없는 경우가 더 많기도 하고요. 따라서 시간복잡도는 영향이 가장 큰 항만을 상수까지 제거해서 나타냅니다. 위 경우 시간복잡도는 \( O(n^2) \)이 되겠네요.
참고로 Big-O 표기법의 엄밀한 정의는 다음과 같습니다.
함수 \( f(n) \)과 \( g(n) \)에 대하여, 양의 상수 \( c \)와 \( n_0 \)가 존재하여 모든 \( n \geq n_0 \)에 대해 \( 0 \leq f(n) \leq c \cdot g(n) \)을 만족할 때, \( f(n) \)은 \( O(g(n)) \)이라고 한다.
위의 \( \frac{n(n-1)}{2} \)을 \( O(n^2) \)로 표현하는 것도 이 정의에 따라 가능합니다. 예를 들어, \( c = 1, n_0 = 2 \)로 잡으면 모든 \( n \geq n_0 \)에 대해
이 성립합니다. 따라서 \( \frac{n(n-1)}{2} \)는 \( O(n^2) \)이 됩니다. 이런 방식으로 엄밀하게 정의할 수도 있지만, 대부분의 경우 최고차항을 남기고 곱해진 상수를 제거하는 방식으로 동일한 결과를 얻을 수 있습니다.
시간복잡도 활용
이제 시간복잡도를 구했으니 필요한 정보를 얻을 차례입니다. 어떤 코드의 시간복잡도가 \( O(n^2) \)라고 합시다. 이때 입력 \( n \)이 최대 100,000이라면 이 코드는 실행에 몇 초 정도가 걸릴 지 예측할 수 있습니다. 일반적으로 1초에 1억(1e8) 번의 연산이 가능하다고 생각하면 됩니다. CPU성능에 따라 다르지만 대부분의 OJ는 CPU 성능을 비슷하게 맞추기 때문에 큰 차이는 없습니다. 따라서 이 예시에서는 \( 10^{10} \)번의 연산이 필요하므로 약 100초가 걸릴 것이라고 예측할 수 있습니다. 따라서 이 코드는 시간초과가 날 것이라고 예측할 수 있습니다.
이번에는 같은 문제에서 최적화를 진행해서 시간복잡도를 \( O(n \log n) \)으로 줄였습니다. 이번에는 \( 10^5 \times 5 \) 정도의 연산이 필요하므로 0.005초 정도가 걸릴 것이고 이 코드는 시간 내에 통과할 것이라고 예측할 수 있습니다. 이제 코드가 올바른 결과를 내주기만 한다면 정답을 받을 수 있겠네요! 이렇게 시간복잡도를 미리 계산해보면 코드가 시간 내에 실행될지 미리 예상해 볼 수 있습니다.
참고로 위의 예시에서 \( \log \)를 밑이 10인 로그로 생각했지만, 대부분 컴퓨터과학에서 등장하는 로그는 밑이 2이거나 \( e \)입니다. 그럼에도 밑을 10으로 계산한 이유는 어떤 밑을 갖는 로그여도 \( \ln n / \ln a \) 형태로 나눌 수 있고, \( \ln a \)는 상수이기 때문에 시간복잡도 계산에서 무시할 수 있기 때문입니다. 대부분의 경우 문제의 제한시간과 시간복잡도의 크기는 굉장히 큰 차이가 나기 때문에 편한대로 계산해도 괜찮습니다.
다른 시간복잡도 표기법
시간복잡도를 표현하는 방법은 여러 가지가 있습니다. 앞서 설명한 Big-O 표기법을 제일 자주 사용하지만 Big-Omega 표기법과 Big-Theta 표기법도 있습니다. Big-Omega 표기법과 Big-Theta 표기법의 수학적인 정의는 각각 아래와 같습니다.
함수 \( f(n) \)과 \( g(n) \)에 대하여, 양의 상수 \( c \)와 \( n_0 \)가 존재하여 모든 \( n \geq n_0 \)에 대해 \( 0 \leq c \cdot g(n) \leq f(n) \)을 만족할 때, \( f(n) \)은 \( \Omega(g(n)) \)이라고 한다.
함수 \( f(n) \)과 \( g(n) \)에 대하여, 양의 상수 \( c_1, c_2 \)와 \( n_0 \)가 존재하여 모든 \( n \geq n_0 \)에 대해 \( 0 \leq c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n) \)을 만족할 때, \( f(n) \)은 \( \Theta(g(n)) \)이라고 한다.
수식을 보면 빅-오 표기법은 \( f(n) \)이 \( g(n) \)보다 작거나 같음을 나타내고, 빅-오메가 표기법은 \( f(n) \)이 \( g(n) \)보다 크거나 같음을 나타냅니다. 빅-세타 표기법은 \( f(n) \)이 \( g(n) \)과 동일한 크기임을 나타냅니다. 즉, 빅-오 표기법은 알고리즘의 실행 시간의 상한을, 빅-오메가 표기법은 실행 시간의 하한을 나타내며, 빅-세타 표기법은 하한과 상한이 일치함을 의미합니다. 일반적으로 최악의 경우가 제일 중요하기 때문에 빅-오 표기법이 가장 자주 사용됩니다. (참고: 최악, 최선, 평균을 의미하는 것이 아닙니다. 참고 글)
시간 복잡도 비교
아래 그래프는 다양한 시간복잡도 함수들의 증가 속도를 비교한 것입니다.
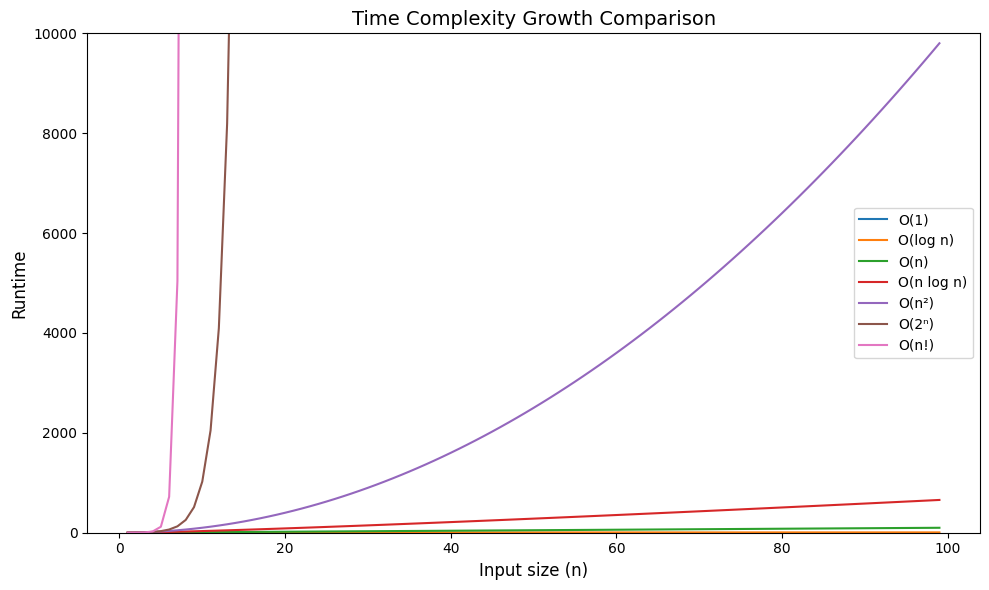
\( n \)이 100까지 커질 때 \( O(\log n) \)은 6.6 정도까지 증가하는 반면 \( O(n^2) \)은 10,000까지 증가했습니다. \( O(2^n) \)은 1,267,650,600,228,229,401,496,703,205,376까지 증가했네요! 참고로 \( O(n!) \)은 100까지 커질 때 약 \( 9.33 \times 10^{157} \)까지 증가합니다. 이 그래프를 통해 알고리즘의 시간복잡도가 얼마나 중요한지 알 수 있습니다. 아래는 자주 사용되는 시간복잡도를 크기 순서대로 나열한 것입니다.