트리
트리는 그래프의 특수한 형태로, 사이클이 없는 연결 그래프입니다. 사이클이 없다는 것은 어떤 두 노드를 잇는 경로가 유일하다는 것을 의미합니다. 연결 그래프는 모든 노드가 서로 연결되어 있다는 뜻입니다. 즉, 아래와 같은 형태의 그래프가 트리입니다.
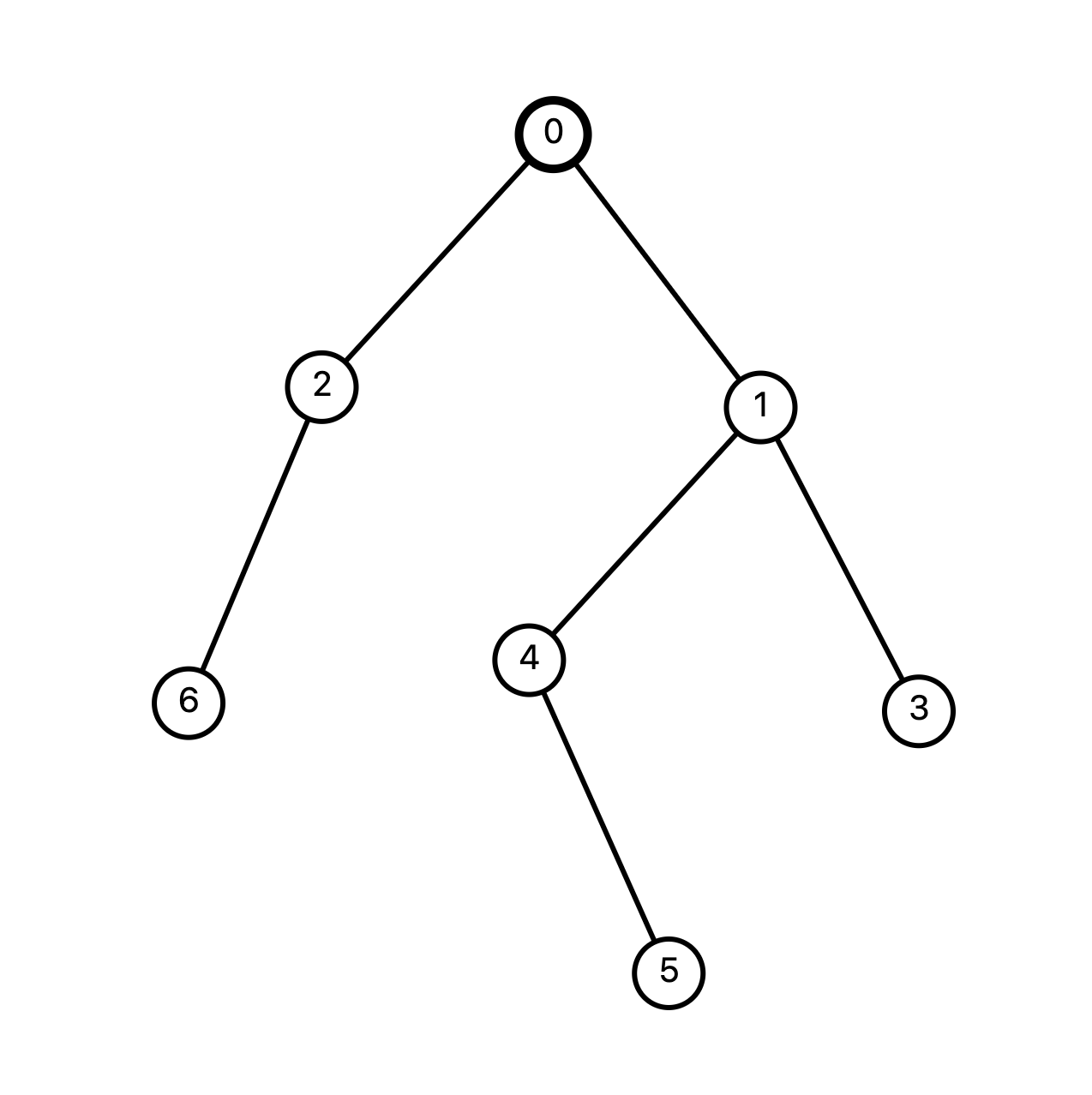
이렇게 그림으로 나타냈을 때 나무처럼 보인다고해서 트리입니다. 위 트리는 0부터 6까지 7개의 노드로 이루어져 있습니다. 간선은 6개입니다. 트리에서 노드의 개수를 \( N \)이라고 할 때, 간선의 개수는 항상 \( N-1 \)입니다. 즉, 트리의 노드 개수는 간선 개수보다 항상 1개 많습니다. 이 성질은 트리의 정의에서 유도할 수 있습니다. 트리는 사이클이 없고 연결 그래프이므로, 노드의 개수가 \( N \)일 때, 간선의 개수는 \( N-1 \)입니다. 만약 간선의 개수가 \( N \)개 이상이라면, 사이클이 생기게 됩니다. 반대로, 간선의 개수가 \( N-2 \)개 이하라면, 연결 그래프를 만들 수 없습니다.
트리에는 root라는 특별한 노드가 있습니다. 루트 노드는 트리의 시작점으로, 모든 노드가 루트 노드를 통해 연결되어 있습니다. 위 그림에서는 0번 노드가 루트 노드로 표현되어 있습니다. 트리는 방향성은 없지만 루트 노드를 기준으로 부모 노드와 자식 노드의 관계를 정의할 수 있습니다. 위 그림에서 1번 2번 노드는 0번 노드의 자식 노드입니다. 1번 노드는 3번과 4번 노드의 부모 노드입니다.
그리고 트리에서 리프 노드(leaf node)라는 개념이 있습니다. 리프 노드는 자식 노드가 없는 노드를 의미합니다. 위 그림에서는 3, 5, 6번 노드가 리프 노드입니다.
1068번 : 트리
BOJ 1068번 문제는 트리에서 특정 노드를 제거했을 때, 남은 트리의 리프 노드 개수를 구하는 문제입니다. 트리는 사이클이 없는 연결 그래프이므로 한 노드를 제거하면 그 노드의 모든 자식 노드도 같이 제거됩니다. 제거된 노드에 주의하면 되는 트리 기본 문제입니다. 여러 접근법이 가능한데, 제가 생각하는 가장 간단한 방법을 소개하겠습니다.
트리는 계층 구조 덕분에 DFS로 탐색하기에 적합합니다. 루트 노드부터 DFS를 진행하는데, 더이상 진행할 노드가 없다면 리프 노드입니다. 다만, 자식 노드가 1개인데 만약 그 유일한 자식 노드가 제거된 노드라면 그 노드는 리프 노드가 됩니다. DFS로 탐색하다가 리프 노드를 만난 순간 그 하위 노드도 전부 제거된 노드이니 바로 리턴하고 다음으로 넘어갑니다. 정답은 여러 종류가 있지만 이 방법이 제가 생각하기에 가장 간단한 방법입니다.
입력이 어떤 노드의 부모로 주어지는데, 이걸 적절히 변형하는 작업이 필요합니다. DFS는 상위에서 하위로 탐색하는데 현재 노드의 자식 리스트를 빠르게 알 수 있어야 효율적이기 때문입니다. 이 부분에 신경써서 코드를 작성하면 됩니다. 아래는 제가 작성한 코드입니다.
#include <bits/stdc++.h>
using namespace std;
void fio() { cin.tie(nullptr); cout.tie(nullptr); ios::sync_with_stdio(false); }
int n;
vector<int> tree[51];
int r;
int dfs(int node) {
if (node == r) return 0;
else if (tree[node].empty())
return 1;
else if (tree[node].size() == 1 && tree[node][0] == r)
return 1;
int sum = 0;
for (int v : tree[node]) {
if (v == r)
continue;
sum += dfs(v);
}
return sum;
}
int main() {
fio();
cin >> n;
int root;
for (int i = 0; i < n; i++) {
int p;
cin >> p;
if (p == -1) {
root = i;
continue;
}
tree[p].push_back(i);
}
cin >> r;
cout << dfs(root);
}
트리의 종류
트리는 형태에 따라 여러 종류로 나눌 수 있습니다. 가장 기본적인 형태는 이진 트리입니다. 이진 트리는 각 노드가 최대 2개의 자식 노드를 가지는 트리입니다. 즉, 자식을 0~2개 가질 수 있습니다. 각 자식은 왼쪽 자식과 오른쪽 자식으로 구분됩니다. 여기서 주의할 점은 자식 노드가 1개인 경우 왼쪽에 있는 경우와 오른쪽에 있는 경우가 다르다는 점입니다. 이진 트리는 이진 탐색 트리, 힙 등 다양한 자료구조에서 사용됩니다.
이진 탐색 트리(Binary Search Tree, BST)는 이진 트리의 일종으로, 어떤 값을 빠르게 찾기 위해 사용되는 트리입니다. 이진 탐색 트리에서는 왼쪽 자식 노드의 값이 부모 노드의 값보다 작고, 오른쪽 자식 노드의 값이 부모 노드의 값보다 큽니다. 이 성질 덕분에 이진 탐색 트리에서는 값을 탐색할 때, 루트 노드부터 시작해서 찾고자 하는 값이 현재 노드의 값보다 작으면 왼쪽 자식으로, 크면 오른쪽 자식으로 이동하면서 탐색할 수 있습니다. 이진 탐색 트리에서의 탐색, 삽입, 삭제는 평균적으로 \( O(\log n) \)의 시간 복잡도를 가집니다. 하지만, 트리가 한쪽으로 치우치게 되면 최악의 경우 \( O(n) \)의 시간 복잡도를 가질 수 있습니다. 이를 방지하기 위해 균형 잡힌 이진 탐색 트리(AVL 트리, 레드-블랙 트리 등)가 고안되었습니다. BST에 대해서는 지금 자세히 다루지는 않겠습니다.
이진 트리에서 모든 노드가 0개 또는 2개의 자식 노드를 가지는 트리를 정 이진 트리(Full Binary Tree)라고 합니다. 즉, 자식 노드가 1개인 노드가 없는 트리입니다.
이진 트리에서 모든 리프 노드가 같은 깊이를 가지고 있고 모든 부모 노드가 2개의 자식 노드를 가지는 트리를 포화 이진 트리(Perfect Binary Tree)라고 합니다. 그림으로 나타내면 아래와 같습니다.
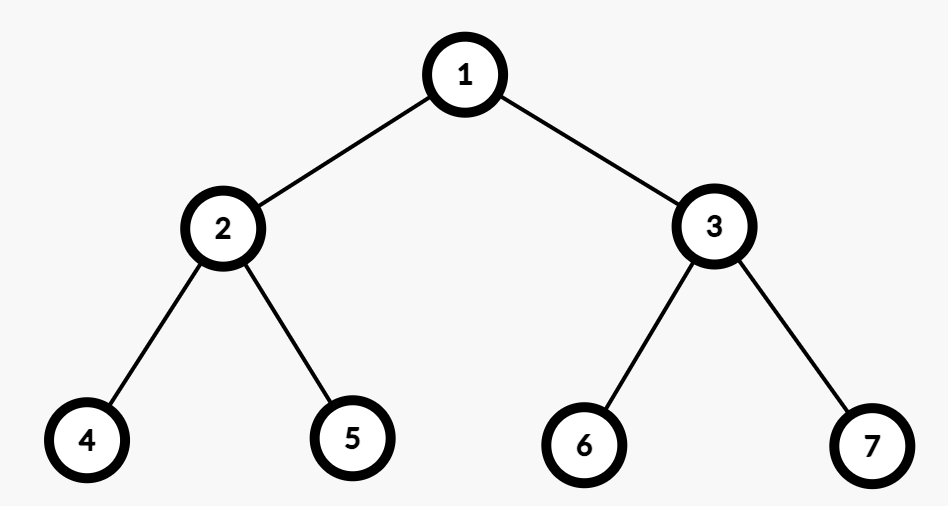
루트 노드가 있는 레벨을 0이라고 할때, 레벨 \( h \)에 있는 노드의 개수는 \( 2^h \)개입니다. 그리고 레벨 \( h \)까지의 모든 노드 개수는 \( 2^{h+1} - 1 \)개입니다. 포화 이진 트리는 정 이진 트리이기도 합니다.
마치며
트리는 굉장히 자주 사용되는 자료구조입니다. 이 글에서는 트리의 기본적인 형태만 알아보았지만 세그먼트 트리, 팬윅 트리, 트라이, 레드-블랙 트리 등 트리를 기반으로 한 다양한 자료구조와 알고리즘이 있습니다. 난이도가 높아서 연습문제에 넣어두지는 않았지만, 비트마스킹을 사용한 트리, 트리 다이나믹 프로그래밍 등 다양한 문제를 앞으로 만나게 될 것입니다.