DFS (Depth-First Search)

깊이 우선 탐색(DFS)은 앞서 살펴본 BFS와 같이 그래프 탐색(graph traversal) 알고리즘 중 하나입니다. BFS가 주변 노드를 우선으로 탐색했다면 DFS는 깊게 들어가는 것을 우선으로 합니다. 다음과 같이 생긴 그래프가 있습니다.

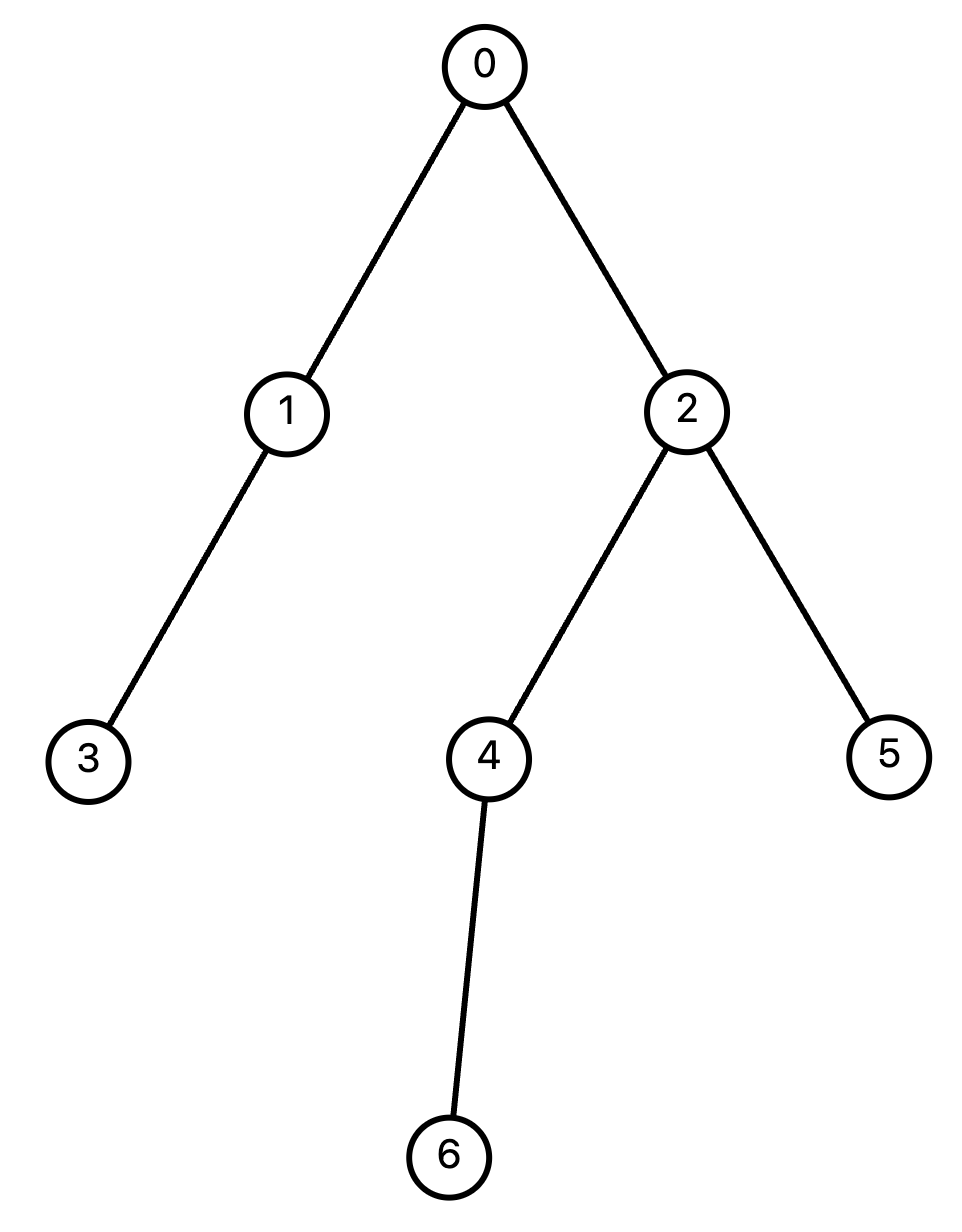
0번부터 시작해서 탐색을 진행해 보겠습니다. 0번 노드에는 인접한 노드가 1, 2가 있습니다. 그 중 1번 노드를 먼저 탐색하기로 했다고 해 봅시다. BFS였다면 1번 노드 다음으로 2번 노드를 탐색했겠지만, DFS는 일단 최대한 깊게 들어갑니다. 따라서 1번 노드에서 인접한 3번 노드로 들어갑니다.

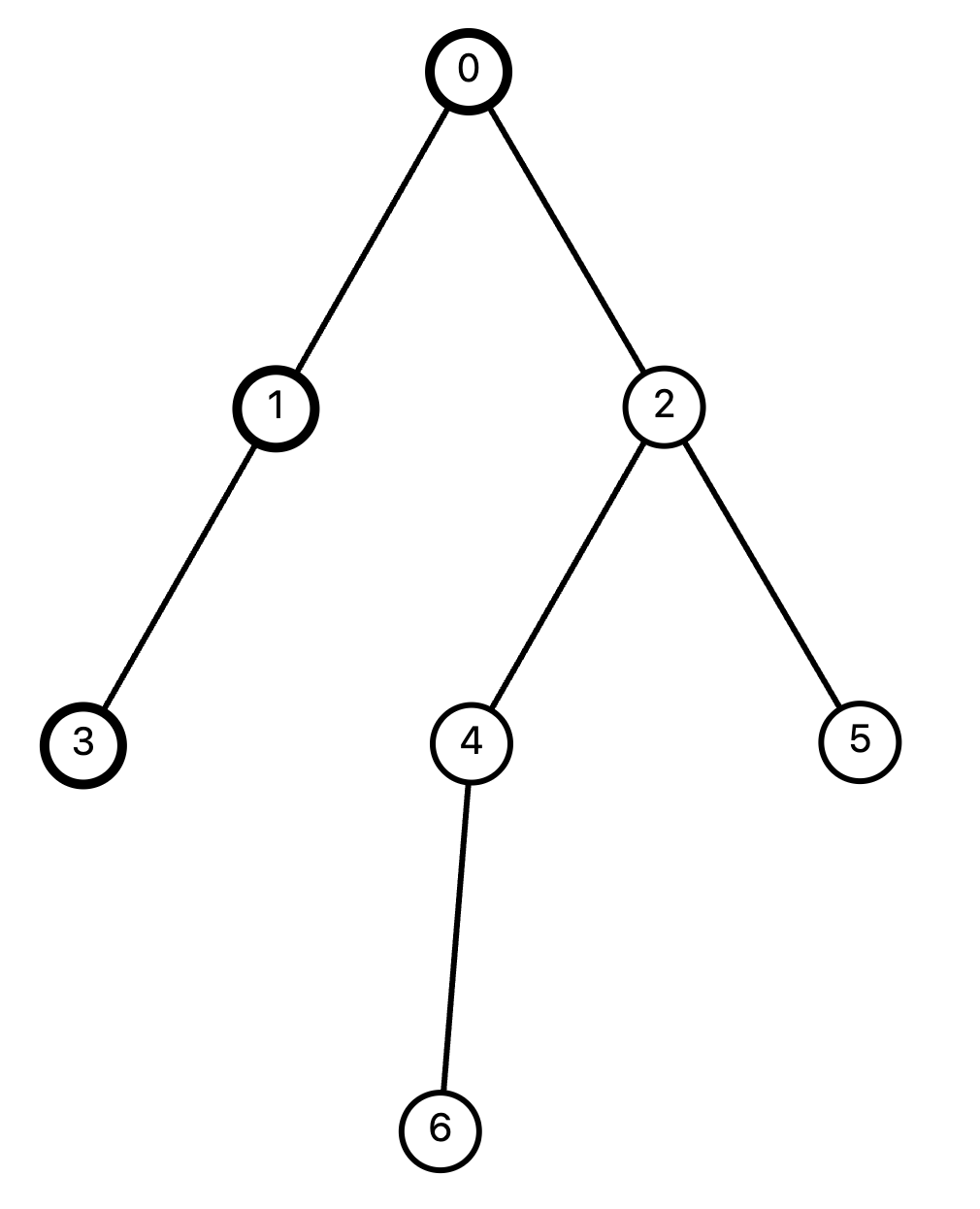
3번 노드에서 더 이상 들어갈 곳이 없으니 다시 돌아옵니다. 1번 노드에서도 더 탐색할 곳이 없으니 0번 노드로 돌아옵니다. 2번 노드가 아직 탐색되지 않았습니다. 2번 노드로 들어갑니다. 2번 노드에서도 최대한 깊게 들어갑니다. 4번 6번 노드까지 들어갑니다.

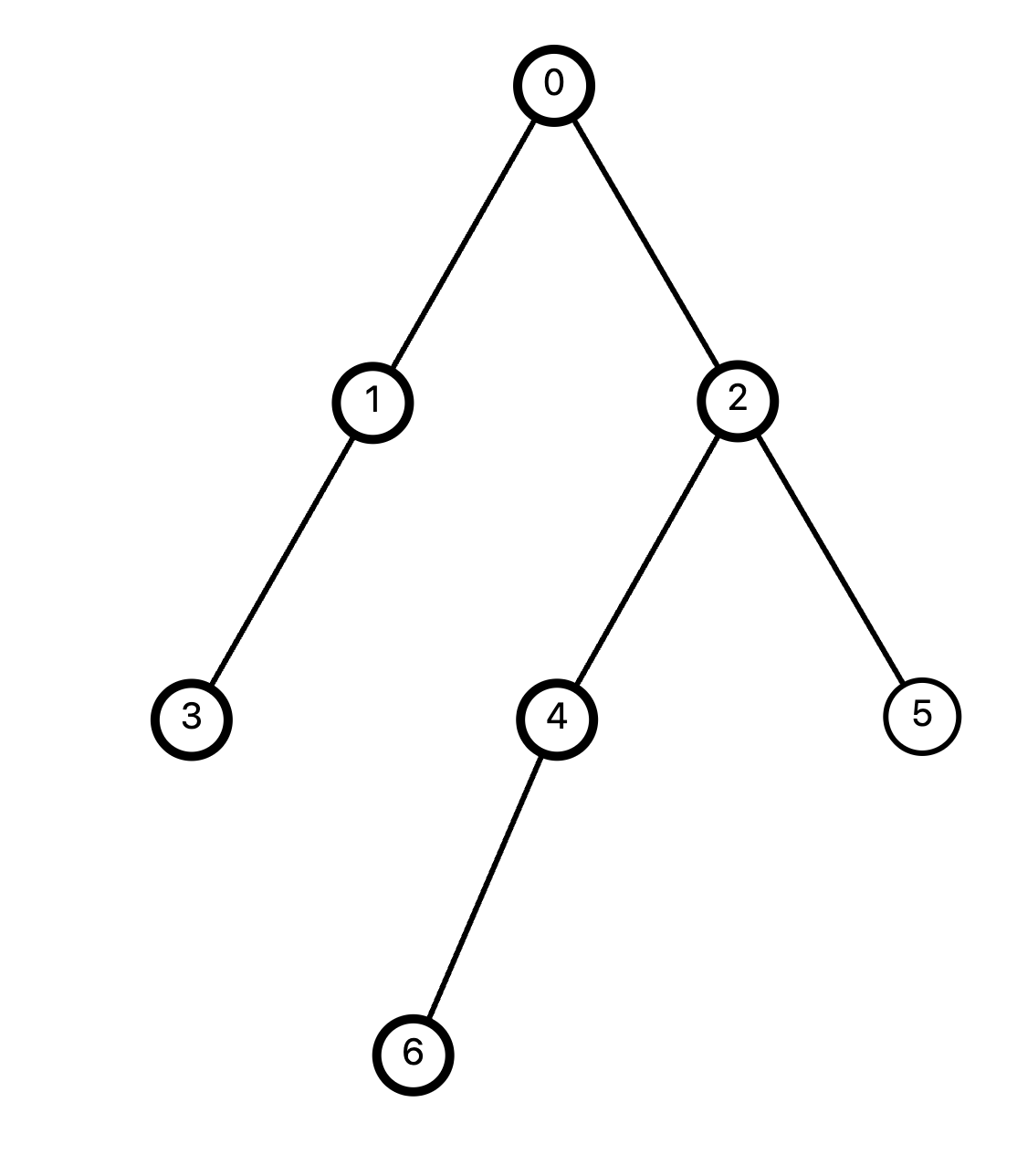
이제 다시 2번 노드까지 돌아와서 마지막 5번 노드를 탐색하고 종료됩니다.

이렇게 DFS는 최대한 깊게 들어간 후 최대한 적게 나와서 다음 탐색을 이어가는 방식입니다. 그러면 어떻게 구현해야 이런 단계를 표현할 수 있을까요? 이것을 보고 재귀나 스택이 떠올랐다면 정답입니다. DFS는 보통 재귀를 통해 구현됩니다. 앞서 살펴본 백트래킹도 일종의 DFS라고 볼 수 있습니다. 참고로 DFS는 스택을 사용해서 구현할 수도 있지만 99% 재귀로 구현합니다. 아래와 같은 그래프가 주어진다고 해 봅시다.

입력

첫 번째 줄에 노드의 개수 \( N \)과 간선의 개수 \( M \)이 주어집니다. 두 번째 줄부터 \( M \)개의 줄에 각각의 간선이 주어집니다. 간선은 두 개의 정수 \( u, v \)로 주어지며, \( u \)와 \( v \)는 연결되어 있습니다. 노드는 0부터 \( N - 1 \)까지의 정수로 표현됩니다. 그래프는 무방향 그래프입니다.

이 그래프에서 DFS를 진행하겠습니다.

vector<vector<int>> adj;
vector<bool> visited;

void dfs(int node) {
    visited[node] = true;
    cout << node << " ";
    for (int neighbor : adj[node]) {
        if (!visited[neighbor]) {
            dfs(neighbor);
        }
    }
}

int main() {
    int n, m;
    cin >> n >> m;
    adj.resize(n);
    visited.resize(n, false);

    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    dfs(0);
}

재귀에 익숙하다면 그렇게 어렵진 않을 것 같습니다. BFS와 DFS 중 아무거나 사용해도 괜찮은 경우도 많지만 목적에 따라 BFS와 DFS를 구분해서 사용해야 할 때도 있습니다. DFS는 백트래킹처럼 완전 탐색과 비슷하게 작동합니다. BFS와 DFS는 정말 빈출 유형이기 때문에 잘 알아두면 좋겠습니다.

DFS

DFS (Depth-First Search)

연습문제